Exercice 4 : Prise en main de BUGS & JAGS

Afin de se familiariser avec le logiciel JAGS (et son interface depuis R via le package rjags), nous nous intéressons ici à l’estimation a posteriori de la moyenne et de la variance d’un échantillon de loi normale.

0. Charger le package rjags.

   library(rjags)

1. Générer \(N=50\) observations selon une loi normale de moyenne \(m=2\) et d’écart-type \(s=3\).

   N <- 50  # le nombre d'observations
   obs <- rnorm(n = N, mean = 2, sd = 3)  # les observations (simulée)

2. Enregistrer dans un fichier .txt le modèle en BUGS défini à l’aide du code suivant :

   # Modèle
   model{
   
     # Vraisemblance
     for (i in 1:N){ 
       obs[i]~dnorm(mu,tau)
     }
   
     # A priori
     mu~dnorm(0,0.0001) # propre mais très plat (faiblement informatif)
     tau~dgamma(0.0001,0.0001) # propre mais très plat (faiblement informatif)
   
     # Variables d'interet
     sigma <- pow(tau, -0.5)
   }

   • Chaque fichier de spécification de modèle doit commencer par l’instruction model{ qui indique à JAGS qu’il s’apprête à recevoir la spécification d’un modèle.
   • Ensuite il faut mettre en place le modèle en bouclant (boucle for) sur l’ensemble des observations. Ici, nous voulons déclarer qu’il y a N observations, et que pour chacune d’entre elle obs[i] suit une loi normale (caractérisée avec la commande dnorm) de moyenne mu et de précision tau.
     ⚠️ Attention : dans BUGS la distribution Normale est paramétrée par sa précision, qui est l’inverse de sa variance (\(\tau = 1/\sigma^2\)).
   • Ensuite, il s’agit de définir les lois a priori pour nos deux paramètres mu et tau, qui sont identiques pour chaque observation. Pour mu, nous prenons un a priori selon la loi normale de moyenne \(0\) et de précision \(10^{-4}\) (donc de variance \(10\,000\) : cela correspond à un a priori faiblement informatif et relativement étalé au vu de l’échelle de nos données). Pour tau nous prenons la loi a priori conjuguée dans un modèle Gaussien, c’est-à-dire la loi Gamma (avec des paramètres très faibles, là encore pour rester le moins informatif possible).
   • Enfin, nous donnons une définition déterministe de paramètre d’intérêt supplémentaire, ici l’écart-type sigma.
     NB: ~ indique une définition probabiliste d’une variable aléatoire, tandis que <- indique une définition par une formule déterministe.

3. À l’aide de la fonction jags.model(), créer un objet jags dans R.

   monpermierjags <- jags.model("normalBUGSmodel.txt", data = list("obs" = obs, 
                                                                   "N" = length(obs)))

   ## Compiling model graph
   ##    Resolving undeclared variables
   ##    Allocating nodes
   ## Graph information:
   ##    Observed stochastic nodes: 50
   ##    Unobserved stochastic nodes: 2
   ##    Total graph size: 58
   ## 
   ## Initializing model

4. À l’aide de la fonction coda.samples(), obtenir un échantillon de taille \(2\,000\) des distributions a posteriori des paramètres de moyenne et d’écart-type.

   res <- coda.samples(model = monpermierjags, variable.names = c("mu", "sigma"), n.iter = 2000)

5. En étudiant le résultat obtenu, calculer les estimateurs de la moyenne a posteriori et de la médiane a posteriori pour mu et sigma et donner un intervalles de crédibilité à 95% pour chacun.

   plot(res)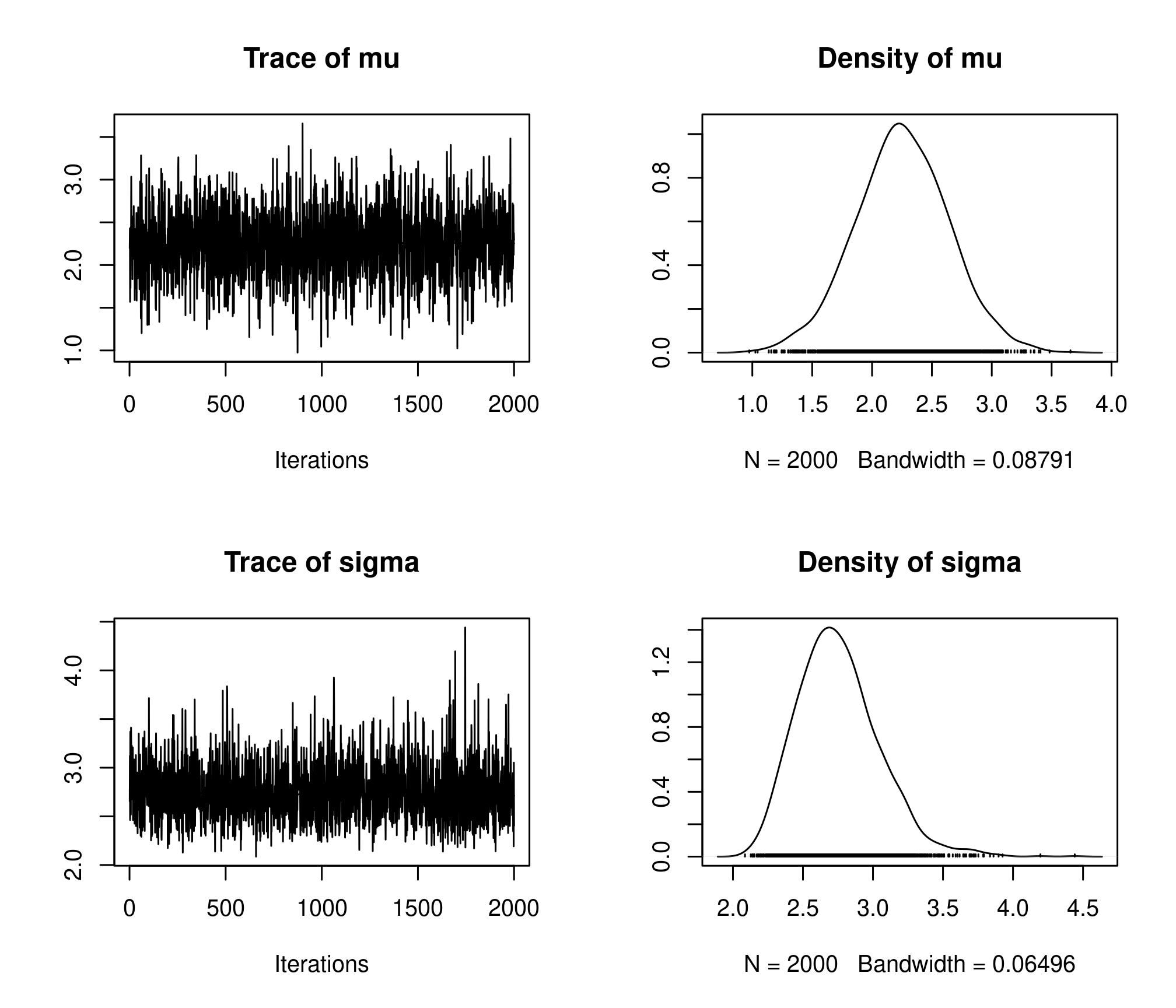

   

   resum <- summary(res)
   resum

   ## 
   ## Iterations = 1:2000
   ## Thinning interval = 1 
   ## Number of chains = 1 
   ## Sample size per chain = 2000 
   ## 
   ## 1. Empirical mean and standard deviation for each variable,
   ##    plus standard error of the mean:
   ## 
   ##        Mean     SD Naive SE Time-series SE
   ## mu    2.251 0.3879 0.008675       0.008512
   ## sigma 2.754 0.2923 0.006536       0.006536
   ## 
   ## 2. Quantiles for each variable:
   ## 
   ##        2.5%   25%   50%   75% 97.5%
   ## mu    1.466 2.000 2.250 2.508 3.031
   ## sigma 2.277 2.551 2.728 2.927 3.393

   resum$statistics["mu", "Mean"]

   ## [1] 2.250648

   resum$statistics["sigma", "Mean"]

   ## [1] 2.754404

   resum$quantiles["mu", "50%"]

   ## [1] 2.249802

   resum$quantiles["sigma", "50%"]

   ## [1] 2.728127

   resum$quantiles["mu", c(1, 5)]

   ##     2.5%    97.5% 
   ## 1.465933 3.031068

   resum$quantiles["sigma", c(1, 5)]

   ##     2.5%    97.5% 
   ## 2.276742 3.393362

6. Charger le package coda. Il s’agit d’un package contenant un certain nombre de fonctions pour le diagnostic de convergence des algorithmes MCMC et le traitement des résultats.

   library(coda)

7. Afin de pouvoir diagnostiquer la convergence d’un algorithme MCMC, il est nécessaire de générer plusieurs chaînes de Markov différentes, partant de valeurs initiales différentes. Recréer un objet jags en spécifiant l’utilisation de 3 chaines de Markov parallèles et en initialisant mu et tau à \((0; -10; 100)\) et \((1; 0,01; 0.1)\) respectivement (ProTip: utiliser une list de list — une pour chaque chaîne). Commenter.

   monjags2 <- jags.model("normalBUGSmodel.txt", data = list(obs = obs, N = N), n.chains = 3,
       inits = list(list(mu = 0, tau = 1), list(mu = -10, tau = 1/100), list(mu = 100,
           tau = 1/10)))

   ## Compiling model graph
   ##    Resolving undeclared variables
   ##    Allocating nodes
   ## Graph information:
   ##    Observed stochastic nodes: 50
   ##    Unobserved stochastic nodes: 2
   ##    Total graph size: 58
   ## 
   ## Initializing model

   res2 <- coda.samples(model = monjags2, variable.names = c("mu", "sigma"), n.iter = 1000)
   plot(res2)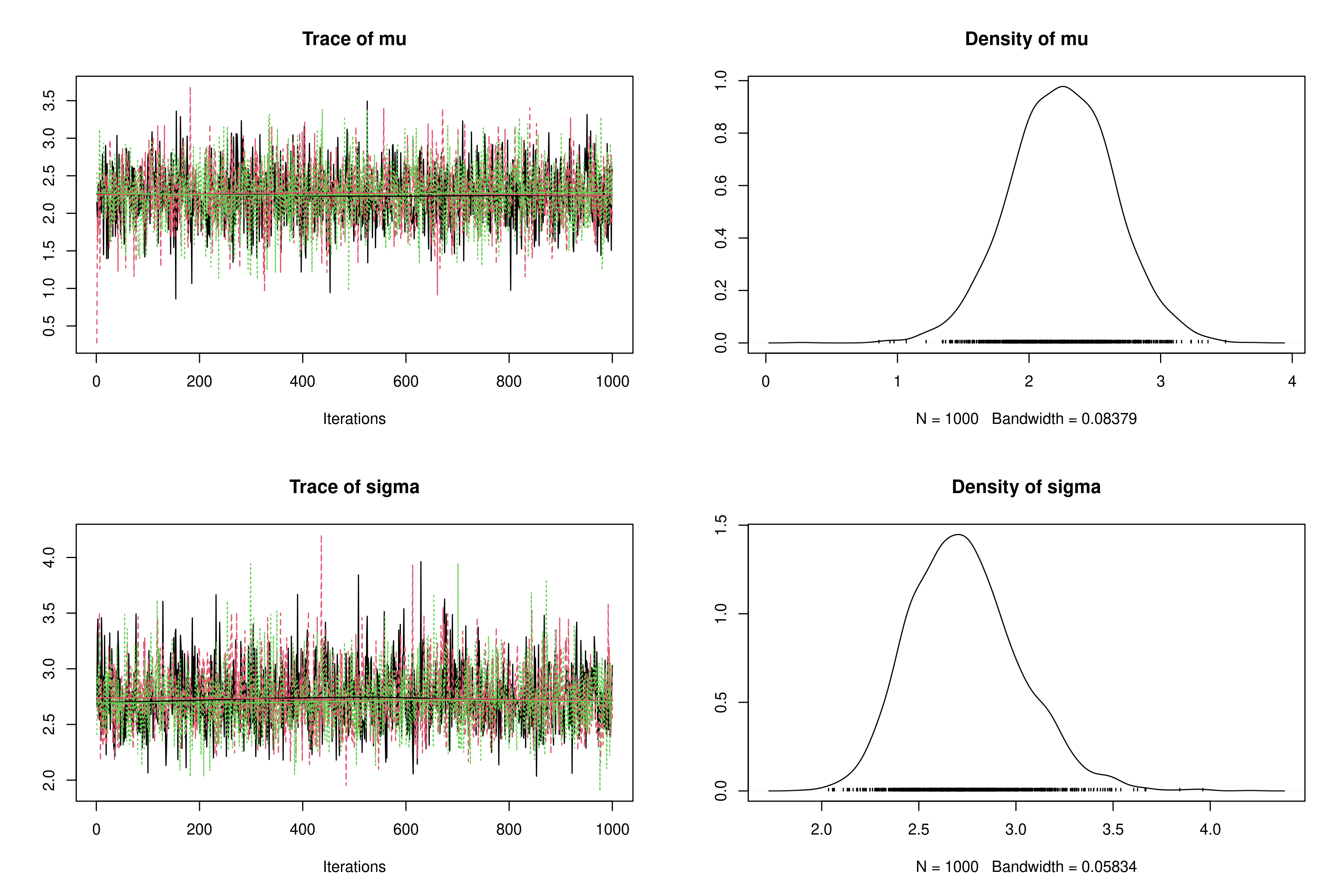

   

8. À l’aide de la fonction gelman.plot(), tracer la statistique de Gelman-Rubin.

   gelman.plot(res2)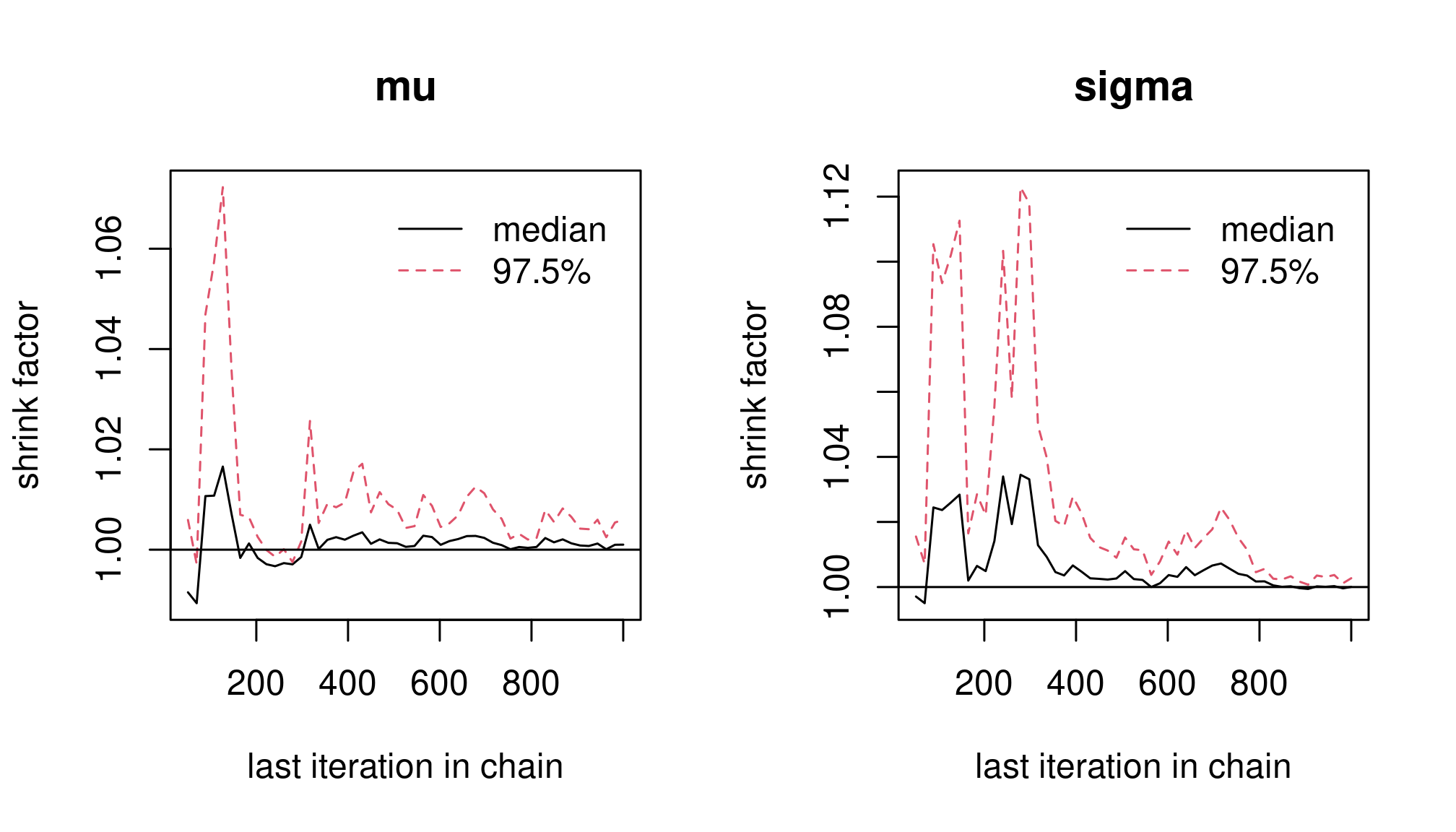

   

9. À l’aide des fonctions autocorr.plot() et acfplot() évaluer l’auto-corrélation des paramètres étudiés.

   acfplot(res2)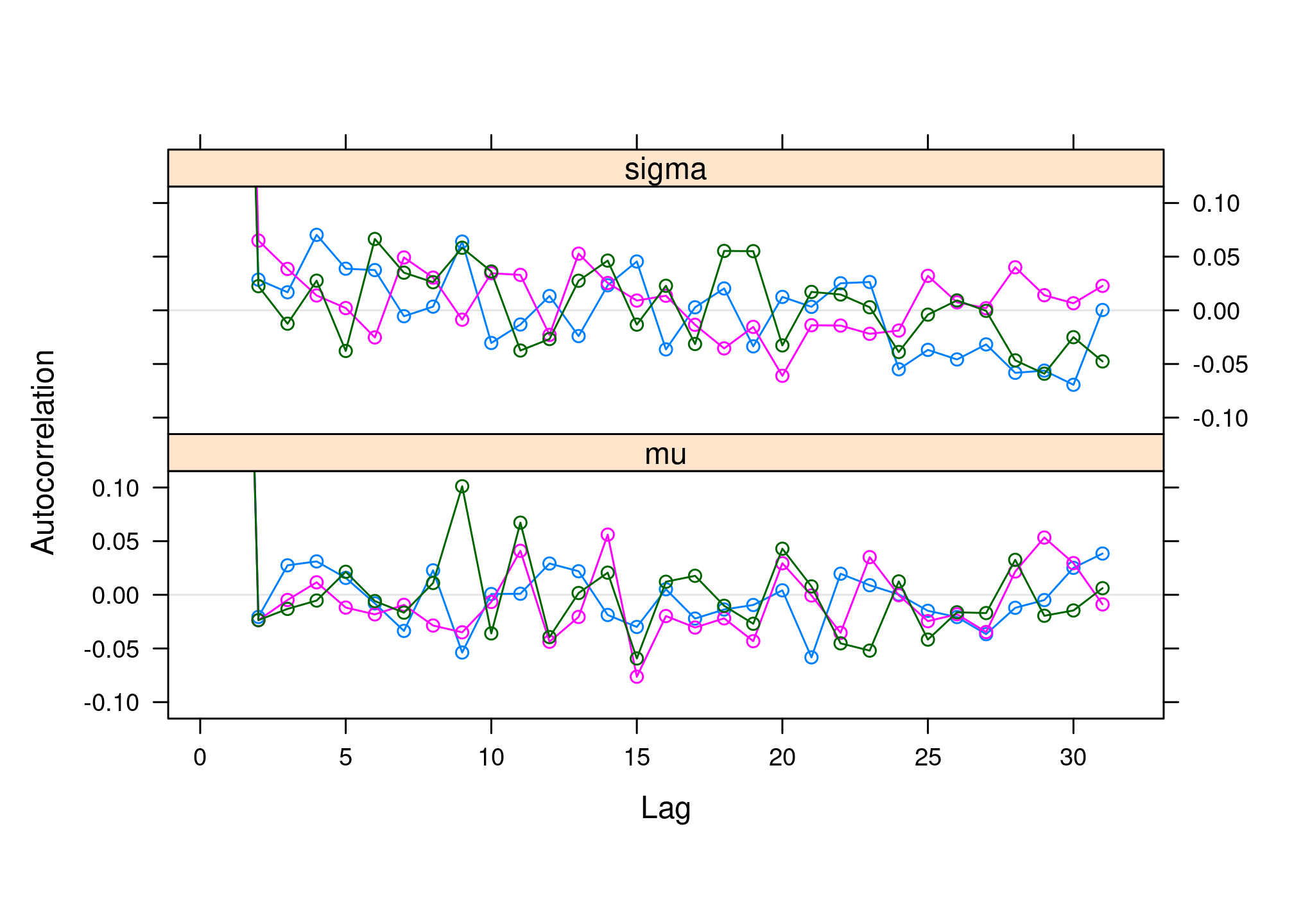

   

   par(mfrow = c(3, 2))
   autocorr.plot(res2, ask = FALSE, auto.layout = FALSE)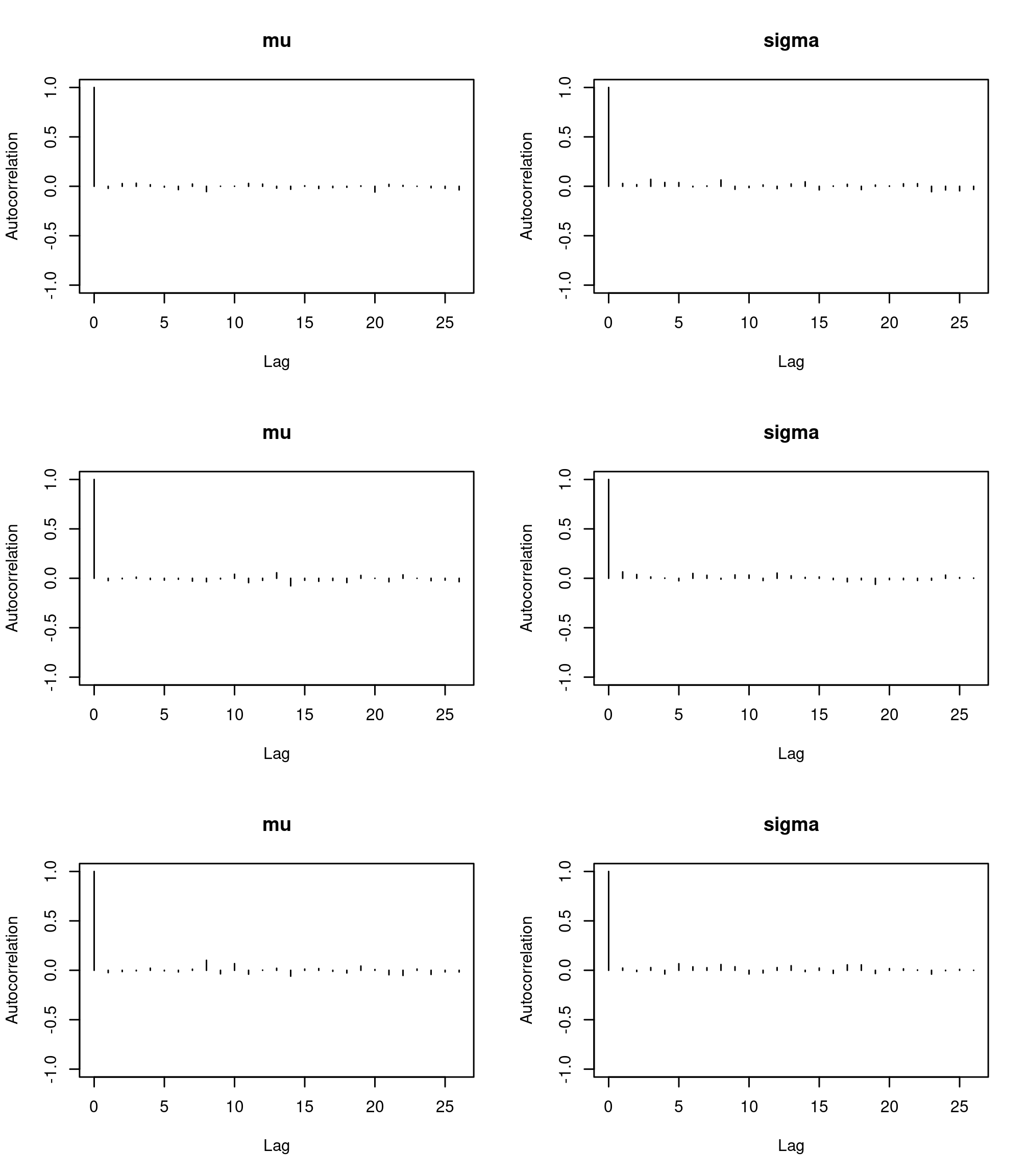

   

10. À l’aide de la fonction cumuplot() évaluer les quantiles cumulés des paramètres étudiés. Comment les interpréter ?

    par(mfrow = c(3, 2))
    cumuplot(res2, ask = FALSE, auto.layout = FALSE)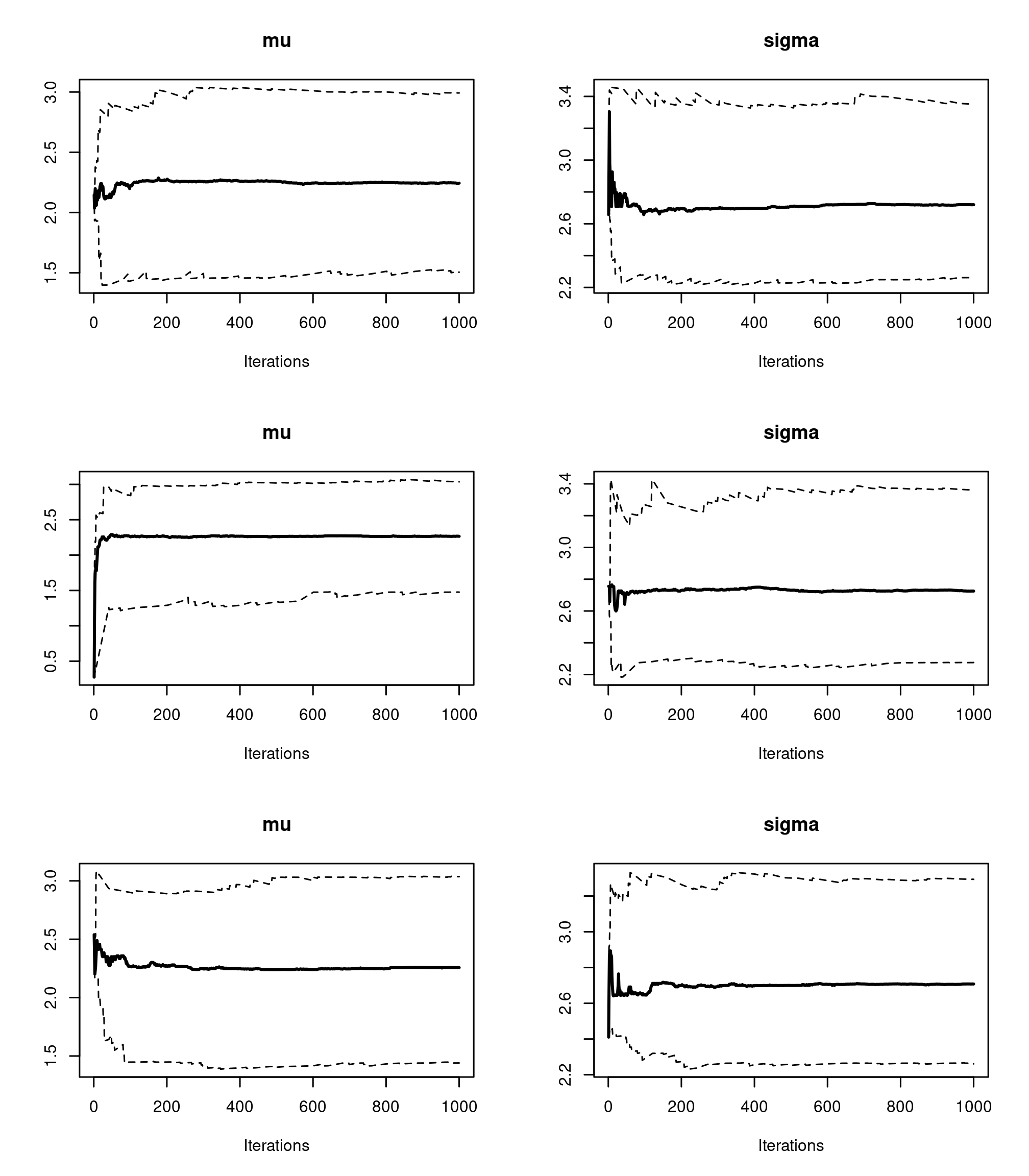

    

11. À l’aide de la fonction crosscorr.plot() évaluer les corrélations entre les paramètres étudiés. Comment les interpréter ?

    crosscorr.plot(res2)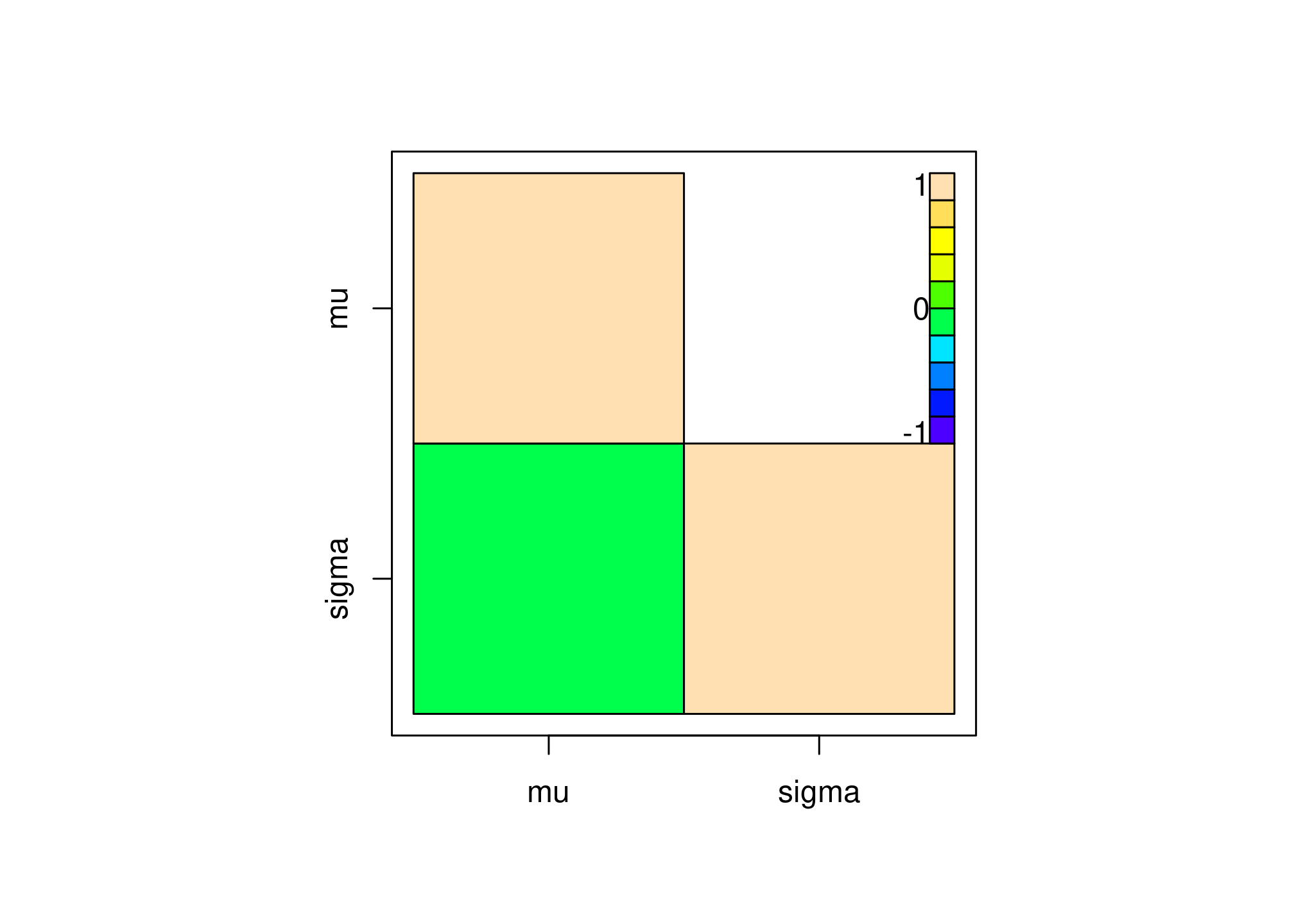

    

12. À l’aide de la fonction hdi() du package HDInterval donner les intervalles de crédibilités de plus haute densité a posteriori à 95%, et les comparer à ceux obtenus à partir des quantiles \(2,5\)% et \(97,5\)%.

    hdCI <- HDInterval::hdi(res2)
    hdCI

    ##             mu    sigma
    ## lower 1.512342 2.248265
    ## upper 3.054642 3.306796
    ## attr(,"credMass")
    ## [1] 0.95

    symCI <- summary(res2)$quantiles[, c(1, 5)]
    symCI

    ##           2.5%    97.5%
    ## mu    1.474634 3.025086
    ## sigma 2.265202 3.335536

    symCI[, 2] - symCI[, 1]

    ##       mu    sigma 
    ## 1.550452 1.070334

    hdCI[2, ] - hdCI[1, ]

    ##       mu    sigma 
    ## 1.542300 1.058532