Les algorithmes MCMC pour l'inférence bayésienne dans la pratique
La mise en place d’algorithmes de Metropolis-Hastings, de Gibbs ou de Metropolis à l’intérieur de Gibbs peut ainsi permettre d’échantillonner selon la loi a posteriori dans le cadre d’un modèle bayésien. On remplace alors JAGS (http://mcmc-jags.sourceforge.net/), STAN (http://mc-stan.org/) ou WinBUGS (https://www.mrc-bsu.cam.ac.uk/software/bugs/the-bugs-project-winbugs/) propose une implémentation de tels algorithmes.
Le projet BUGS (Bayesian inference Using Gibbs Sampling : https://www.mrc-bsu.cam.ac.uk/software/bugs/) a été initié en 1989 par l’unité de Biostatistique du MRC (Medical Research Council) de l’Université de Cambridge (au Royaume-Uni) afin de proposer un logiciel flexible pour l’analyse bayésienne de modèles statistique complexe à l’aide d’algorithmes MCMC. Son implémentation la plus connue est WinBUGS, un logiciel clic-bouton disponible sous le système d’exploitation Windows. OpenBUGS est une implémentation fonctionnant sous Windows, Mac OS ou Linux. JAGS (Just another Gibbs Sampler) est une autre implémentation plus récente qui s’appuie également sur le langage BUGS. Une ressource très utile est le manuel de l’utilisateur de JAGS (http://sourceforge.net/projects/mcmc-jags/files/Manuals/3.x/jags_user_manual.pdf). Enfin, il faut également noter le logiciel STAN, récemment développé à l’Université de Columbia qui n’est similaire à BUGS que dans son interface, s’appuyant sur des algorithmes MCMC innovants, comme par exemple les approches de Monte-Carlo Hamiltonien ou l’approche variationnelle.
Convergence des algorithmes MCMC
L’échantillonnage selon la distribution a posteriori par un algorithme MCMC comporte 2 phases :
La phase de chauffe (burn-in) :
elle correspond aux premières itérations de l’algorithme MCMC, qui ne doivent pas être conservées dans l’analyse de l’échantillon de Monte-Carlo. En effet, celles-ci ne proviennent pas de la distribution stationnaire. Cette phase correspond donc au temps nécessaire à la chaîne de Markov pour converger vers sa loi stationnaire. Sa longueur varie d’un modèle à l’autre. Il n’y a aucune conséquence à prendre une phase de chauffe trop longue, si ce n’est son coût computationnel.La phase d’échantillonnage :
elle doit être suffisamment longue pour permettre une bonne estimation de la distribution a posteriori, notamment concernant les plages de valeurs de faible probabilité.
Les propriétés mathématiques des chaînes de Markov garantissent la convergence des algorithmes MCMC, mais sans donner d’indication sur le nombre d’itérations de l’algorithme nécessaire pour atteindre cette convergence. S’il n’existe aucun moyen de garantir cette convergence en temps fini, il existe un certain nombre d’outils permettant de diagnostiquer la non-convergence d’une chaîne de Markov vers sa loi stationnaire. Il faut donc les utiliser de concert lors de l’interprétation des sorties d’un algorithme MCMC afin d’éviter les situations où la chaîne n’a pas convergé.
Une manière de surveiller la convergence d’un algorithme d’échantillonnage MCMC est de générer plusieurs chaînes (de façon parallèle et indépendante) avec des valeurs initiales différentes. Si l’algorithme fonctionne, alors ces différentes chaînes (de Markov) doivent converger vers la même distribution stationnaire (la loi a posteriori). Après suffisamment d’itérations, il devrait être impossible de faire la distinction entre ces différentes chaînes. Pour chaque chaîne, les
Erreur de Monte-Carlo
L’erreur de Monte-Carlo caractérise l’incertitude introduite par l’échantillonnage MCMC. Pour un paramètre donné (comme par exemple l’estimation d’une moyenne a posteriori), elle quantifie la variabilité attendue dans son estimation si nous générerions plusieurs chaînes, c’est-à-dire plusieurs échantillons de Monte-Carlo a posteriori (grâce à un algorithme MCMC, avec différentes initialisations et à chaque fois un même nombre
Taille d’échantillon effective
Un échantillon généré à partir d’un algorithme MCMC n’est
Un solution employée en pratique pour diminuer ces problèmes d’auto-corrélation est de ne pas conserver toutes les valeurs échantillonnées successivement par un algorithme MCMC, mais d’espacer les itérations conservées. Par exemple, on pourra ne conserver que les valeurs échantillonnées toutes les 2, 5, ou 10 itérations, ce qui permettra de diminuer la dépendance au sein de l’échantillon de Monte-Carlo généré.
Statistique de Gelman-Rubin
Une façon d’évaluer la convergence d’un échantillonneur MCMC est de comparer la variation entre les différentes chaînes à la variation à l’intérieur d’une même chaîne après un certain nombre d’itérations. Si l’algorithme a bien convergé, la variation inter-chaîne doit être proche de zéro.
Soit
avec
La statistique Gelman-Rubin est un ratio (donc sans unité) ce qui en fait un résumé s’interprétant simplement et de la même manière pour tout échantillonneur MCMC. Autre avantage, il ne nécessite pas de choisir au préalable un paramètre à estimer (contrairement aux erreurs de Monte-Carlo). La statistique de Gelman-Rubin est donc un bon moyen de diagnostiquer la convergence d’un algorithme MCMC. Néanmoins, son calcul peut être instable et elle ne peut garantir la convergence à elle seule. Il s’agit d’un outil pour la surveillance plus générale d’une chaîne de Markov.
À noter que d’autres statistiques (par exemple la statistqiue de Geweke) sont parfois utilisées à la place ou en complément de celle de Gelman-Rubin, qui reste la plus populaire.
Diagnostiques graphiques
En complément de la statistique de Gelman-Rubin, un certain nombre de diagnostiques graphiques peuvent permettre de diagnostiquer la non convergence d’un algorithme MCMC :
la trace : désigne la représentation des valeurs successives de la chaîne. Lorsque l’on génère plusiquers chaîne indépendante à partir d’initialisations différentes, les traces des différentes chaînes doivent se stabiliser et se superposer une fois la convergence atteinte.
estimateur de densité non-paramétrique (à noyau) : d’après le théorème de convergence de Bernstein-von Mises, la distribution a posteriori doit être unimodale. Pour cela on peut utiliser un estimateur de densité non-paramétrique (à noyau) sur l’échantillon de Monte-Carlo généré afin de vérifier que la loi a posteriori est bien unimodale et suffisamment lisse.
les quantiles courants : de la même façon que la trace, les quantiles des différentes chaînes doivent se stabiliser et se superposer au cours des différentes itérations une fois la convergence atteinte.
le diagramme de Gelman-Rubin : on représente la statistique de Gelman-Rubin cumulée au cours des différentes itérations. Son niveau doit rapidement se retrouver très proche de 1 (idéalement
l’auto-corrélation : Lorsque la chaîne de Markov ne “mixe” pas très bien, il peut arriver que les observations successives soient fortement corrélées d’une itération à la suivante. Cela n’est pas un problème en soit, mais cela diminue fortement la taille d’échantillon effective pour l’estimation a posteriori. Une solution courante est de ne conserver qu’une itération sur
thin, réglant l’espacement entre les itérations conservées dans l’échantillon MCMC).la corrélation croisée : On peut également s’intéresser à la corrélation entre nos différents paramètres à travers les différents échantillons a posteriori. À noter qu’il est fréquent d’observer une forte corrélation entre certains paramètres et que ce n’est pas nécessairement indicatif d’un problème avec l’algorithme MCMC (dans l’approche fréquentiste on estime également des corrélations – parfois importantes – entre les paramètres d’un modèle, grâce à la matrice d’information de Fisher).
Remarque : il est fréquent que les diagnostiques soient satisfaisants pour certains paramètres, mais ne le soient pas pour d’autres. Il s’agit d’une appréciation subjective, et l’objectif est que la majorité des critères soient satisfaits (ou plus ou moins satisfaits) pour une grande majorité des paramètres.
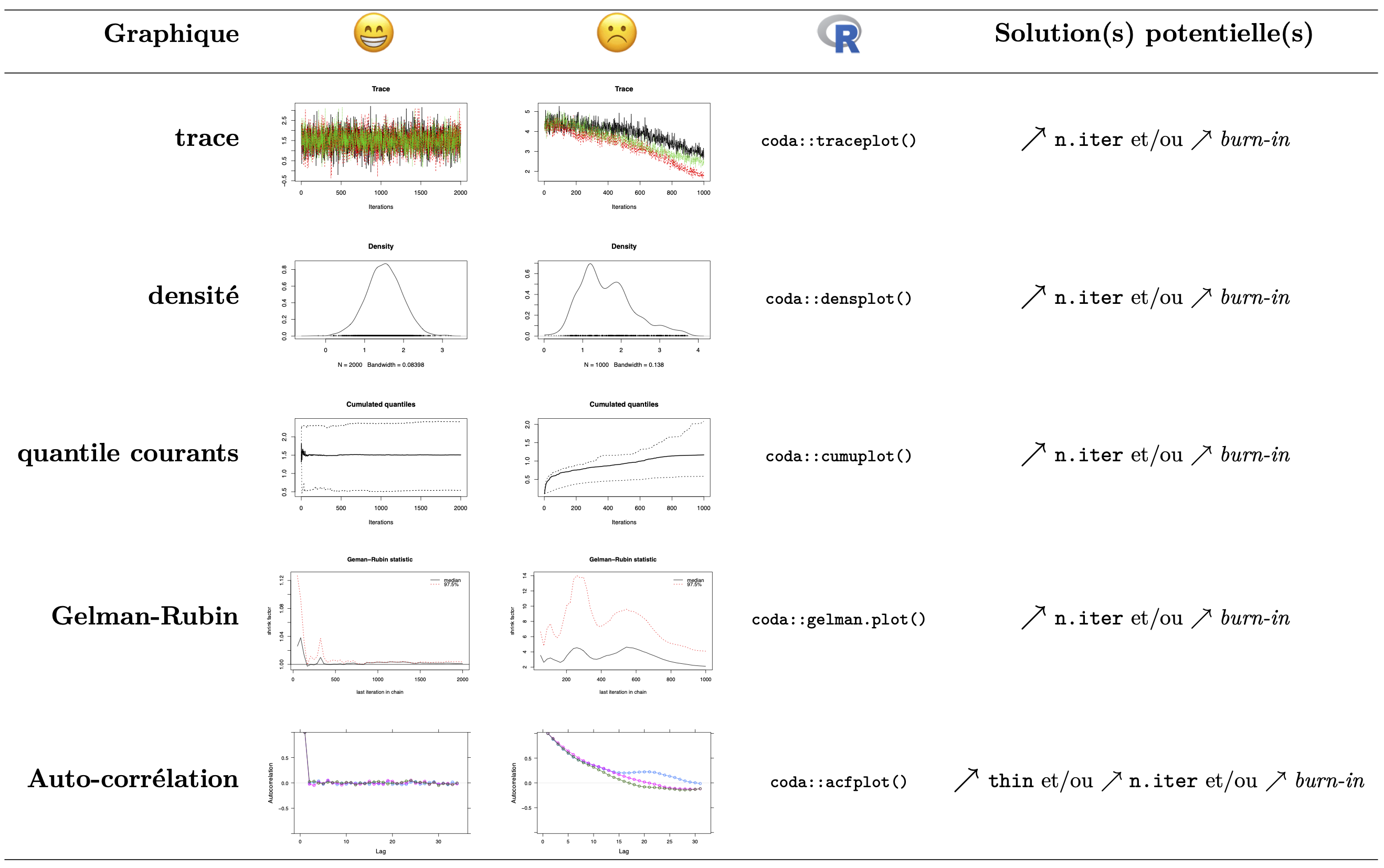
Figure 1: Exemples de référence pour les diagnostiques graphiques de convergence
Inférence à partir d’échantillonnage MCMC
Estimation
Grâce aux algorithmes MCMC, on est donc capable d’obtenir un échantillon de Monte-Carlo de la loi a posteriori pour un modèle bayésien donné. On peut donc utiliser la méthode de Monte-Carlo pour obtenir différentes estimations a posteriori : estimation ponctuelle (moyenne a posteriori, médiane a posteriori, …), intervalle de crédibilité (notamment grâce au package HDInterval qui permet de calculer l’intervalle de crédibilité le plus étroit pour un niveau de crédibilité donné, c’est-à-dire le Highest Density Interval —
Deviance Information Criterion (
Le Deviance Information Criterion (
M Plummer, Penalized loss functions for Bayesian model comparison, Biostatistics, 2008↩︎