Méthodes d'échantillonnage directes

Génération de nombres aléatoires selon des lois de probabilité usuelles
Échantillonner selon une loi définie analytiquement

Génération de nombres aléatoires selon des lois de probabilité usuelles

Il existe plusieurs manières de générer des nombres dits “aléatoires” selon des lois connues. La très grande partie des programmes informatiques ne génèrent pas des nombres totalement aléatoires. On parle plutôt de nombres pseudo-aléatoires, qui semblent aléatoires mais sont en réalité générés selon un processus déterministe (qui dépend notamment d’une “graine”).

La distribution uniforme

Pour générer un échantillon pseudo-aléatoire selon la loi uniforme sur $[0; 1]$ , on peut donner l’exemple de l’algorithme congruentiel linéaire (Lehmer, 1948) :

Générer une suite d’entiers $y_{n}$ tel que :
$y_{n + 1} = (a y_{n} + b) mod. m$
$x_{n} = \frac{y_{n}}{m - 1}$

Choisir $a$ , $b$ et $m$ de manière à ce que $y_{n}$ ait une période très longue et que $(x_{1}, \dots, x_{n})$ puisse être considéré comme $i i d$

où $y_{0}$ est appelé la “graine” (seed en anglais). On remarque que l’on a necessairement $0 \leq y_{n} \leq m - 1$ . En pratique on prend $m$ très grand (par exemple $2^{19937}$ , la valeur par défaut dans R qui utilise l’algorithme Mersenne-Twister). Dans ce cours, on ne va pas plus s’intéresser à la génération de nombre pseudo-alétoires selon la loi uniforme sur $[0; 1]$ , il s’agit d’un outil que l’on considère fiable et qui est utilisé par les différents algorithmes présentés par la suite.

Autres distributions

Pour échantillonner selon la loi binomiale $B i n (n, p)$ , on peut utiliser les relations entre les différentes lois usuelles en partant de $U_{i} \sim U_{[0; 1]}$ : $\begin{aligned} Y_{i} & = 1_{U_{i} \leq p} \sim Bernoulli (p), \\ X & = \sum_{i = 1}^{n} Y_{i} \sim B i n (n, p) \end{aligned}$

Pour échantillonner selon la loi normale $N (0, 1)$ , on peut utiliser l’algorithme de Box-Müller:
Si $U_{1}$ et $U_{2}$ sont 2 variables uniformes $[0; 1]$ indépendantes, alors $\begin{aligned} Y_{1} & = \sqrt{- 2 \log U_{1}} \cos (2 π U_{2}) \\ Y_{2} & = \sqrt{- 2 \log U_{1}} \sin (2 π U_{2}) \end{aligned}$ sont indépendantes et suivent chacune la loi normale $N (0, 1)$ .

Échantillonner selon une loi définie analytiquement

Méthode par inversion

Inverse généralisée
Pour une fonction $F$ définie sur $R$ , on définit son inverse généralisée par $F^{- 1} (u) = inf {x; F (x) > u}$

Soit $F$ la fonction de répartition d’une distribution de probabilité, et soit $U$ une variable aléatoire suivant une loi uniforme sur $[0; 1]$ . Alors $F^{- 1} (U)$ définit une variable aléatoire ayant pour fonction de répartition $F$ .

On déduit de la propriété ci-dessus que si l’on connaît la fonction de répartition de la loi selon laquelle on veut simuler, et si l’on est capable de l’inverser, alors on peut générer un échantillon suivant cette loi à partir d’un échantillon uniforme sur $[0; 1]$ .

On veut générer un échantillon suivant la loi exponentielle de paramètre $λ$
On a la densité de la loi exponentielle qui est $f (x) = λ e x p (- λ x)$ , et la fonction de répartition (son intégrale) qui vaut $F (x) = 1 - e x p (- λ x)$ .
Posons $F (x) = u$ . On remarque alors que $x = - \frac{1}{λ} \log (1 - u)$ .
Si $U \sim U_{[0; 1]}$ , alors $X = F^{- 1} (U) \sim E x p (λ)$ .

Méthode d’acceptation-rejet

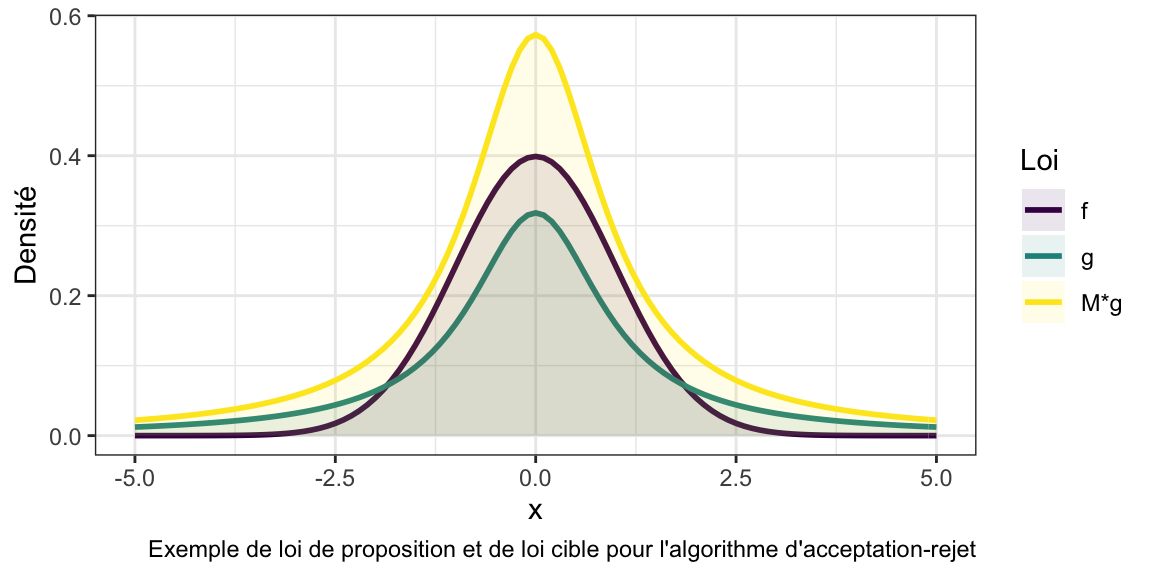
La méthode d’acceptation-rejet consiste à utiliser une loi instrumentale $g$ , dont on sait échantillonner selon la loi, afin d’échantillonner selon la loi cible $f$ . Le principe général est de choisir $g$ proche de $f$ et de proposer des échantillons selon $g$ , d’en accepter certains et d’en rejeter d’autres afin d’obtenir un échantillon suivant la loi de $f$ .

Soit une loi d’intérêt de densité $f$ .
Soit une loi de proposition de densité $g$ (à partir de laquelle on sait échantillonner) telle que, pour tout $x$ : $f (x) \leq M g (x)$ Pour $i = 1, \dots, n$ :

Générer $x_{i} \sim g$ et $u_{i} \sim U_{[0; 1]}$
Si $u_{i} \leq \frac{f (x_{i})}{M g (x_{i})}$ on accepte le tirage:
$y_{i} := x_{i}$
sinon on le rejette et on retourne en 1.

$(y_{1}, \dots, y_{n}) \overset{i i d}{\sim} f$

Plus $M$ est petit, plus le taux de rejet est faible et plus l’algorithme est efficace (au sens où il nécessite moins d’itérations pour obtenir un échantillon de taille $n$ ). On a donc intérêt à choisir $g$ le plus proche possible de $f$ , en particulier lorsque la dimension augmente (l’impact de $M$ étant d’autant plus important alors). Néanmoins, la loi de proposition aura nécessairement des queues plus lourdes que la loi cible, et ce dans toutes les dimensions de l’espace des paramètres. À cause du fléau de la dimension, lorsque le nombre de paramètres augmente, le taux d’acceptation décroit très rapidement.

👉 Exercice 1 : Construire un pseudo-échantillon de taille $n$ selon la loi discrète suivante (multinomiale à $m$ éléments ${x_{1}, \dots, x_{m}}$ ) : $P (X = x) = p_{1} δ_{x_{1}} (x) + p_{2} δ_{x_{2}} (x) + \dots p_{m} δ_{x_{m}} (x) avec \sum_{i = 1}^{m} p_{i} = 1 et δ_{a} (x) = 1_{{x = a}}$

Pour $i = 1, \dots, n$ :

échantillonner selon la loi uniforme : $u_{i} \sim U_{[0, 1]}$
$y_{i} := x_{min {j; u_{i} \in [0; \sum_{l = 1}^{j} p_{l}]}}$

$(y_{1}, \dots, y_{n}$ ) est alors un pseudo-échantillon de taille $n$ de la loi $M u l t (p_{1}, \dots, p_{m})$

👉 Exercice 2 : Grâce à la méthode par inversion, générer un pseudo-échantillon de taille suivant une loi de Cauchy (dont la densité est $\forall x \in R$ $f (x) = \frac{1}{π (1 + x^{2})}$ ), sachant que $\arctan^{'} (x) = \frac{1}{(1 + x^{2})}$ et que $lim_{x \to - \infty} a r c t a n (x) = - \frac{π}{2}$ .

$F (y) = \int_{- \infty}^{y} f (x) d x$

Alors $F (x) = \frac{\arctan (x)}{π + 1 / 2}$ , et il suit que $F^{- 1} (x) = \tan (π (x - 1 / 2))$ .

Donc $Y = \tan (π (U - 1 / 2)) \sim Cauchy$ (avec $U \sim U_{[0, 1]}$ ), et on en déduit l’algorithme suivant :

Pour $i = 1, \dots, n$ :

échantillonner selon la loi uniforme : $u_{i} \sim U_{[0, 1]}$
$y_{i} := \tan (π (u_{i} - 1 / 2))$

$(y_{1}, \dots, y_{n}$ ) est alors un pseudo-échantillon de taille $n$ de la loi de Cauchy

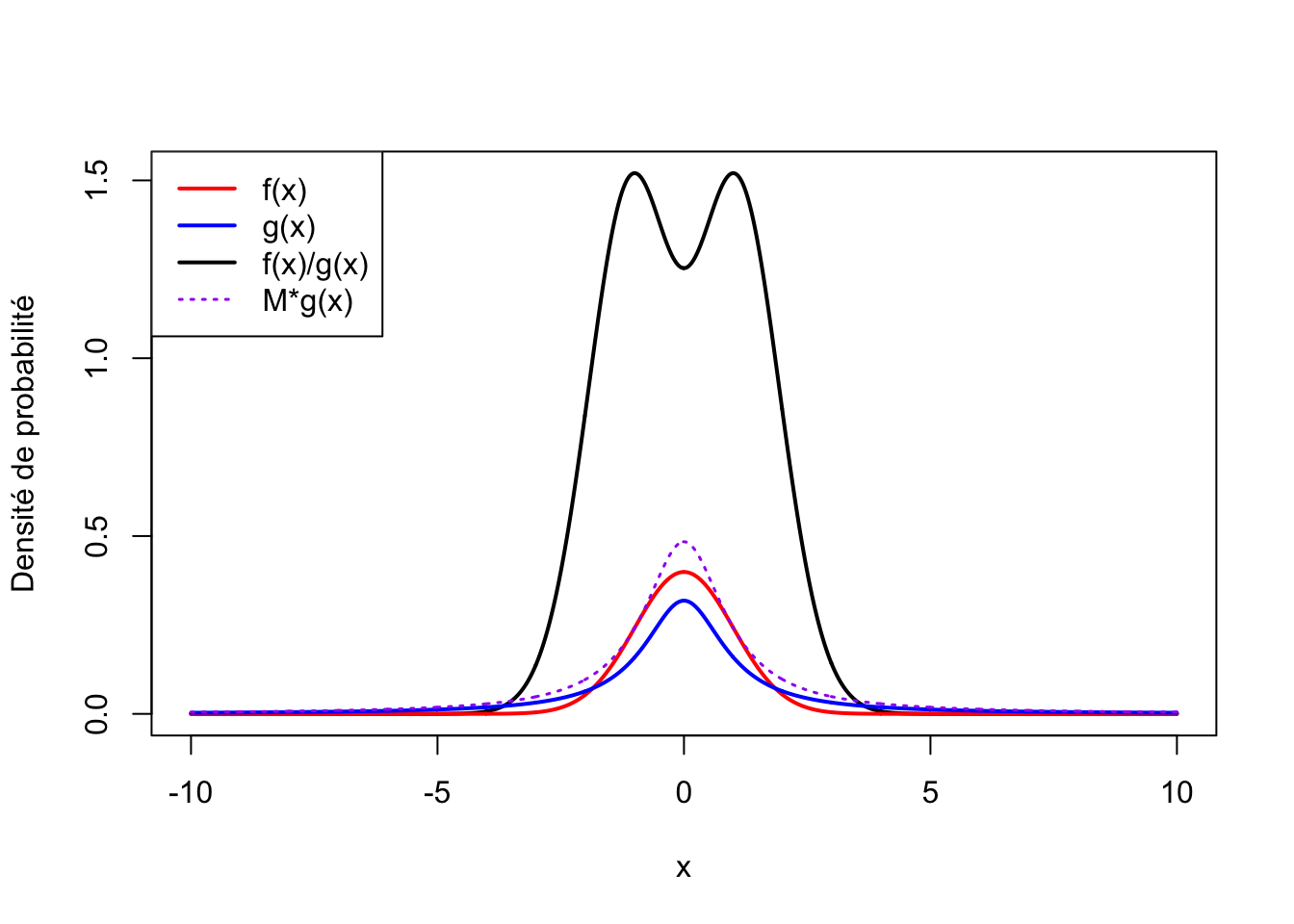
👉 Exercice 3 : Écrire un algorithme d’acceptation-rejet pour simuler la réalisation d’un pseudo-échantillon de taille $n$ d’une loi normale $N (0, 1)$ en utilisant une loi de Cauchy comme proposition. Trouvez la valeur de $M$ optimale.

$f (x) = \frac{\exp (- x^{2} / 2)}{\sqrt{2 π}}$ et $g (x) = \frac{1}{π (1 + x^{2})}$

On cherche $M$ le plus petit possible tel que $M \geq \frac{f (x)}{g (x)} \forall x$ .

En dérivant $\frac{f (x)}{g (x)}$ , on trouve $max (\frac{f (x)}{g (x)})$ pour $x = - 1$ ou $x = 1$ (la dérivée s’annule en -1,0, et 1). Donc $\frac{f (x)}{g (x)} \leq \sqrt{\frac{2 π}{e}}$

On va donc utiliser : $M = \sqrt{\frac{2 π}{e}}$

f <- function(x){
  exp(-x^2/2)/sqrt(2*pi)
}
g <- function(x){
  1/(pi*(1+x^2))
}
x <- seq(from = -10, to = 10, by = 0.01)
plot(x=x, y=f(x)/g(x), type='l', lwd = 2, ylab="Densité de probabilité")
lines(x = x, y=f(x), type = "l", lwd = 2, col="red")
lines(x = x, y=g(x), type = "l", lwd = 2, col="blue")
lines(x = x, y=g(x)*sqrt(2*pi/exp(1)), type = "l", lwd = 1.5, lty=3, col="purple")
legend("topleft", legend = c("f(x)", "g(x)", "f(x)/g(x)", "M*g(x)"), col=c("red", "blue", "black", "purple"), lwd=c(2, 2, 2, 1.5), lty=c(1, 1, 1, 3))

Dernière mise à jour le 29/11/2021