Inférence bayésienne
Une fois la modélisation bayésienne terminée, on dispose de la distribution a posteriori (obtenue grâce au choix de la distribution a priori, du modèle d’échantillonnage et des données observées). Cette distribution contient l’ensemble de l’information sur \(\theta\) conditionnellement au modèle et aux données. On peut néanmoins s’intéresser à des résumés de cette distribution, par exemple à un paramètre central de cette distribution tel que l’espérance, le mode ou encore la médiane (ces derniers sont analogues aux estimateurs ponctuels obtenus par l’analyse fréquentiste), où à des intervalles de valeurs dont la probabilité a posteriori est forte.
Théorie de la décision
La théorie de la décision statistique est généralement utilisée dans un contexte d’estimation d’un paramètre inconnu \(\theta\). La décision concerne alors le choix d’un estimateur ponctuel \(\widehat{\theta}\). Afin de déterminer le \(\widehat{\theta}\) optimal, on définit une fonction de coût (à valeur dans \([0, +\infty[\)) représentant la pénalité associée au choix d’un \(\widehat{\theta}\) particulier (c’est-à-dire à la décision associée). Afin de déterminer le \(\widehat{\theta}\) optimal (c’est-à-dire la décision optimale) on va vouloir minimiser la fonction de coût choisie. À noter qu’un grand nombre de fonctions de coût différentes sont possibles, et que chacune d’entre elle résulte en un estimateur ponctuel optimal différent et donc une décision optimale spécifique.
L’espérance a posteriori
L’espérance a posteriori est définie par : \[\mu_P = \mathbb{\mathbb{E}}(\theta|\boldsymbol{y}) = \mathbb{E}_{\theta|\boldsymbol{y}}(\theta)\] À noter que le calcul de cette espérance a posteriori n’est pas toujours facile car il suppose le calcul d’une intégrale…
C’est l’estimateur qui minimise l’erreur moyenne quadratique a posteriori (ou coût quadratique). En effet, pour un estimateur quelconque \(\hat{\theta}\), l’erreur quadratique moyenne a posteriori se décompose comme : \[\mathbb{E}_{\theta}\left[(\hat{\theta} - \theta)^2 | \boldsymbol{y}\right] = \hat{\theta}^2 -2\hat{\theta}\mathbb{E}_{\theta}\left[\theta | \boldsymbol{y}\right] + \mathbb{E}_{\theta}\left[\theta^2 | \boldsymbol{y}\right]\] En dérivant l’expression ci-dessus par rapport à \(\hat{\theta}\), on montre aisément que le minimum est obtenu pour \(\hat{\theta} = \mathbb{E}_{\theta}\left[\theta | \boldsymbol{y}\right]\).
Le maximum a posteriori
Le maximum a été beaucoup utilisé, surtout car il est plus facile (ou en tout cas moins difficile) à calculer. En effet, il ne requiert aucun calcul d’intégrale, mais une simple maximisation de \(f(\boldsymbol{y}|\theta)\pi(\theta)\) (car le dénominateur \(f(\boldsymbol{y})\) ne dépend pas de \(\theta\)). L’estimateur du mode s’appelle le maximum a posteriori (souvent noté MAP).
Le MAP peut être vu comme une régularisation (par la loi a priori) de l’estimateur du maximum de vraisemblance, dont il est proche.
La médiane a posteriori
La médiane est également un résumé possible de la distribution a posteriori. Comme son nom l’indique, il s’agit de la médiane de \(p(\theta | \boldsymbol{y})\). Il s’agit de l’estimateur ponctuel optimal au sens de l’erreur absolue (fonction de coût linéaire).
L’intervalle de crédibilité
Finalement on peut définir un ensemble de valeurs ayant une forte probabilité a posteriori. Un tel ensemble est appelé ensemble de crédibilité. Si la loi a posteriori est unimodale, un tel ensemble est un intervalle. Par exemple, un intervalle de crédibilité à 95% est un intervalle \([t_{inf};t_{sup}]\) tel que \(\textstyle\int_{t_{inf}}^{t_{sup}} p(\theta|\boldsymbol{y})\,\text{d}\theta = 0.95\). En général on est intéressé par l’intervalle de crédibilité à 95% le plus étroit possible (Highest Density Interval).
On rappelle ici l’interprétation d’un intervalle de confiance fréquentiste au niveau 95%, qui s’interprète comme suit, par rapport à l’ensemble des intervalles de ce niveau qu’on aurait pu observer : …
…
…
…
⚠️ on ne peut pas interpréter une réalisation d’un intervalle de confiance en terme probabiliste ! C’est une erreur qui est souvent commise… L’intervalle de crédibilité s’interprète lui bien plus naturellement, comme un intervalle qui a 95% de chance de contenir \(\theta\) (pour un niveau de 95%, évidemment).
Distribution prédictive
La distribution prédictive (appelée parfois posterior predictive) est définie comme la distribution d’une nouvelle observation \(Y_{n+1}\) sachant les observations de l’échantillon. Elle se calcule comme la distribution de \(Y_{n+1}\) sachant \(\boldsymbol{y}\), marginalement par rapport à \(\theta\). Sa densité \(f_{Y_{n+1}} (y|\boldsymbol{y}) = \int f_{Y}(y|\theta)p(\theta|\boldsymbol{y}) \,\text{d}\theta\) se calcule ainsi, en supposant les nouvelles observations conditionnellement indépendantes des anciennes sachant \(\theta\) : \[\begin{align*} f_{Y_{n+1}}(y|\boldsymbol{y}) &= \int_\Theta f_{Y_{n+1}} (y, \theta|\boldsymbol{y}) \,\text{d}\theta\\ &= \int_\Theta f_{Y_{n+1}} (y|\theta, \boldsymbol{y})p(\theta|\boldsymbol{y}) \,\text{d}\theta\\ &= \int_\Theta f_{Y_{n+1}} (y|\theta)p(\theta|\boldsymbol{y}) \,\text{d}\theta\\ &= \int_\Theta f_{Y} (y|\theta)p(\theta|\boldsymbol{y}) \,\text{d}\theta \end{align*}\] On remarque le lien entre cette formule et celle de la distribution marginale des données : \(f_Y(y) = \textstyle \int f_Y(y|\theta)\pi(\theta) \,\text{d}\theta\), qui peut être vue comme un cas particulier de la distribution prédictive quand il n’y a pas d’information apportée par l’échantillon observé. On note également la différence avec l’approche fréquentiste où l’on estime d’abord \(\theta\) par \(\hat{\theta}\), et l’on remplace \(\theta\) par \(\hat{\theta}\) pour obtenir la distribution prédictive : \(f_{Y_{n+1}} (y|\hat{\theta})\).
Exercice : calculer la distribution prédictive sur l’exemple historique du sexe à la naissance pour un a priori uniforme.
Facteur de Bayes
Le Facteur de Bayes correspond au ratio des vraisemblances marginales de 2 hypothèses (par exemple \(H_1\) et \(H_0\)) : \[BF_{H_1\text{ vs }H_0} = \frac{f(\boldsymbol{y}| H_1)}{f(\boldsymbol{y}| H_0)}\] Il s’interprète en termes de préférence pour l’une ou l’autre des deux hypothèses considérées à partir des données observées \(\boldsymbol{y}\). Dans le cadre d’une analyse bayésienne, on peut l’utiliser afin de faire de la sélection de modèle, en particulier pour quantifier l’apport d’un paramètre additionnel dans le modèle. Jeffreys a proposé une échelle pour interpréter la valeur du facteur de Bayes.
| Valeur du facteur de Bayes | Interprétation |
|---|---|
| \(BF < 1\) | Négatif (en faveur de \(H_0\)) |
| \(1 \leq BF < 10^{1/2}\) | Mérite à peine d’être mentionné |
| \(10^{1/2} \leq BF < 10\) | Substantiel |
| \(10 \leq BF < 10^{3/2}\) | Fort |
| \(10^{3/2} \leq BF < 100\) | Très fort |
| \(100 \leq BF\) | Décisif |
La cote a posteriori (posterior odds) de \(H_1\) par rapport à \(H_0\) peut alors se calculer comme : \[\frac{p(H_1 | \boldsymbol{y})}{p(H_0 | \boldsymbol{y})} = BF_{H_1\text{ vs }H_0} \times \frac{p(H_1)}{p(H_0)}.\] Si la probabilité a priori est identique pour les deux hypothèse (c’est-à-dire que \(p(H_0) = p(H_1)\)), alors la cote a posteriori est égale au facteur de Bayes.
Propriétés asymptotiques – et fréquentistes – de la distribution a posteriori
Théorème de convergence de Doob
Un résultat très intéressant est le comportement asymptotique de la distribution a posteriori sous certaines hypothèses (cas \(iid\), densités dérivables trois fois, existence de moments d’ordre 2). Il y a un premier résultat, le théorème de convergence de Doob, qui assure que la distribution a posteriori se concentre vers la “vraie” valeur (au sens fréquentiste) du paramètre quand \(n \rightarrow \infty\). On peut le noter (convergence en Loi) : \[p(\theta|\boldsymbol{y}_n) \overset{\mathcal{L}}{\rightarrow} \delta_{\theta^*}\]
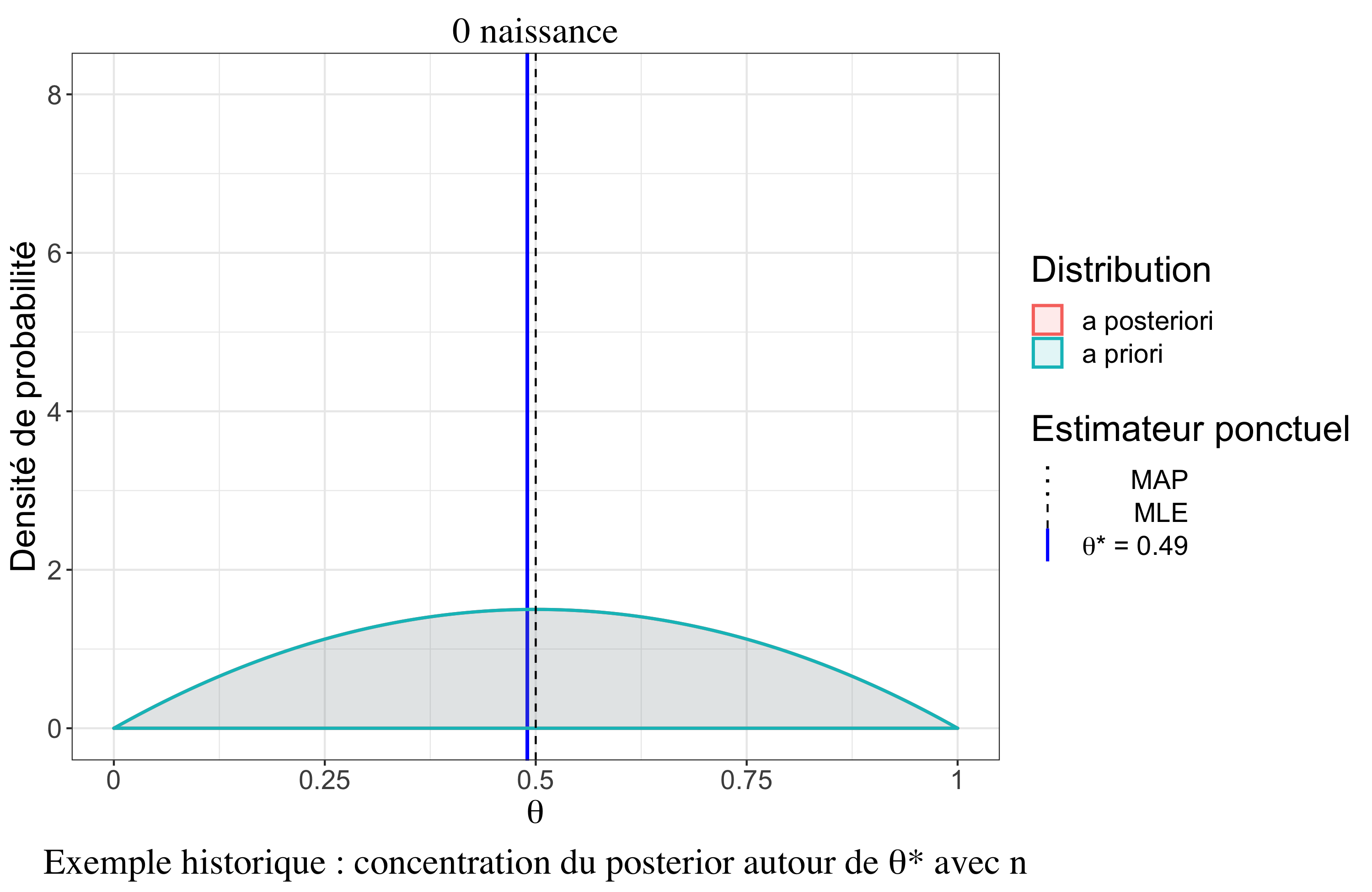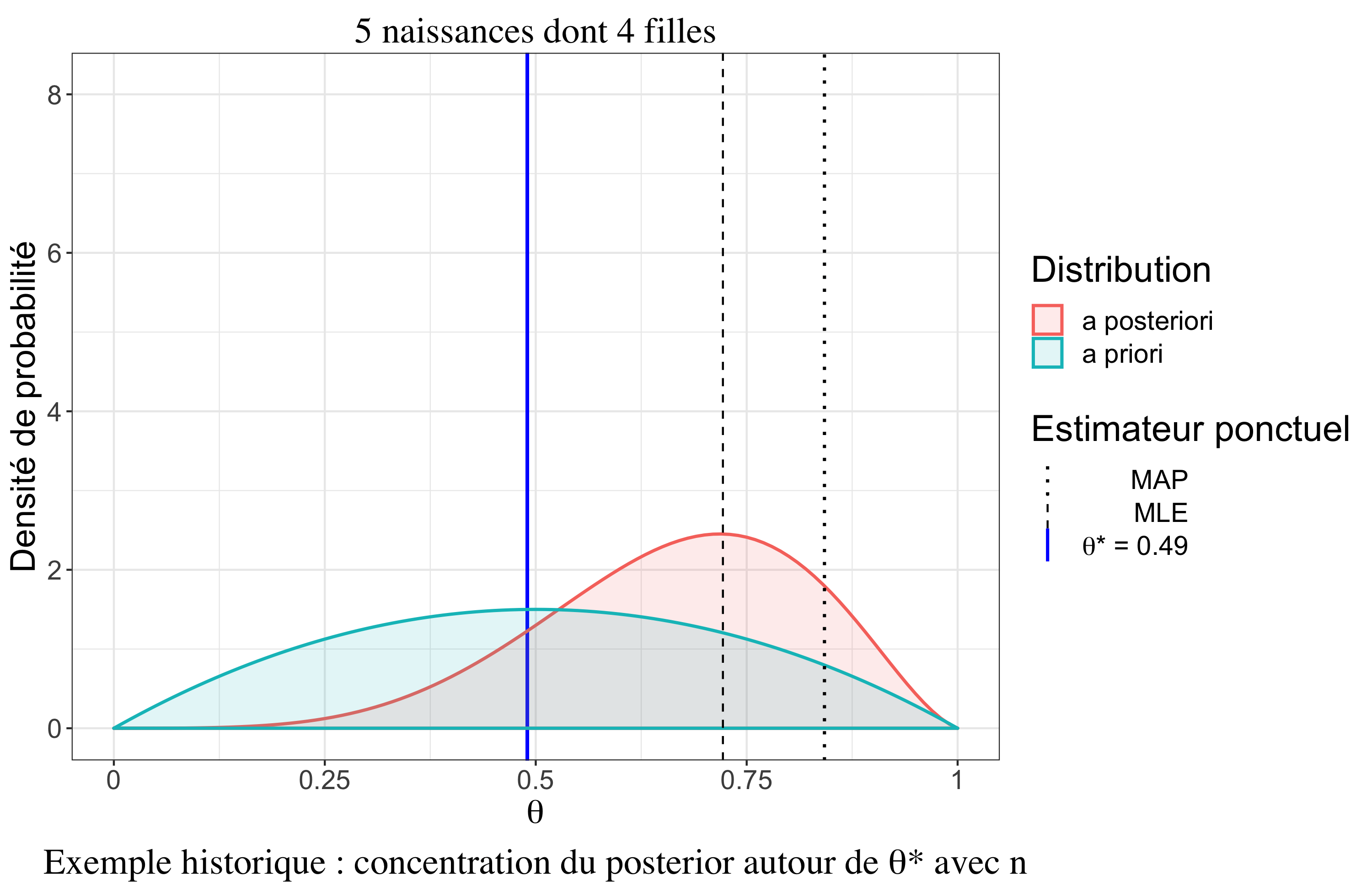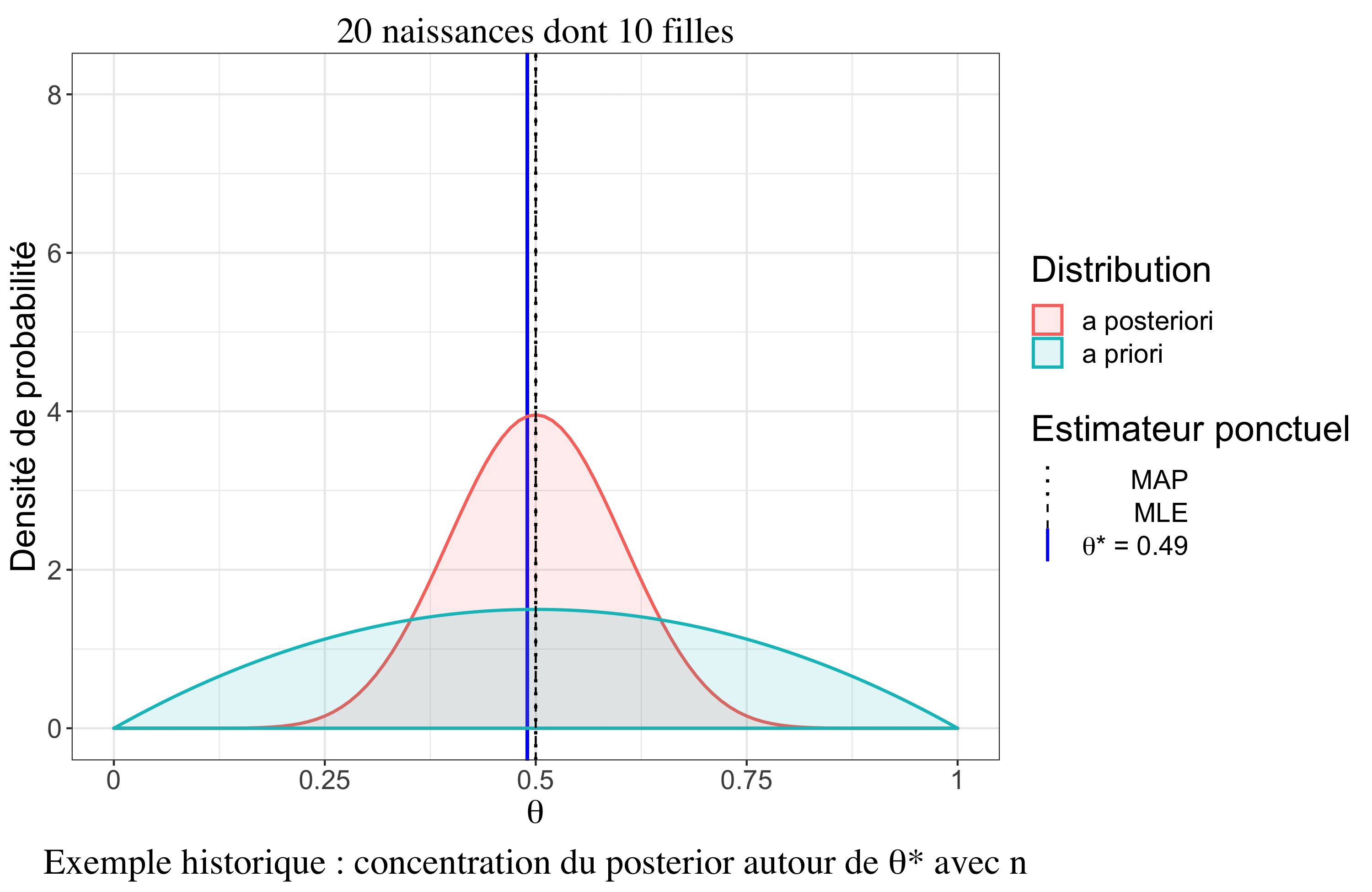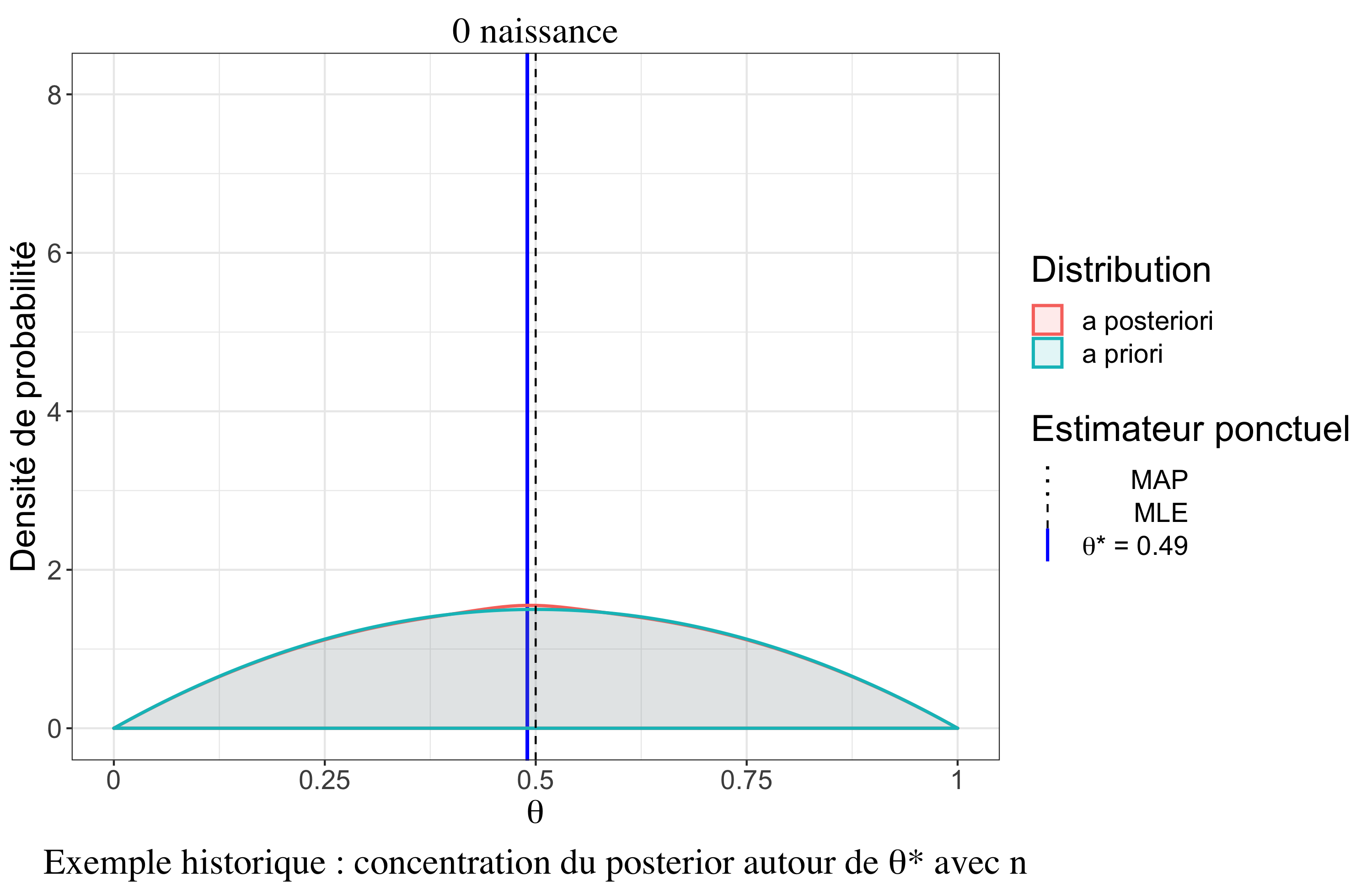
Théorème de Bernstein-von Mises
Un résultat plus riche caractérise la distribution asymptotique de \(\theta\) : le Théorème de Bernstein-von Mises (aussi appelé Théorème limite central bayésien). Pour \(n\) grand la distribution a posteriori \(p(\theta|\boldsymbol{y})\) peut être approximée par une loi normale ayant pour espérance le mode \(\hat{\theta}\) et pour variance l’inverse de la Hessienne (dérivée seconde) de \(p(\theta|\boldsymbol{y})\) par rapport à \(\theta\), pris au mode \(\hat{\theta}\).
Ci-dessous une démonstration heuristique, grâce à un développement limité de \(\log(p(\theta|\boldsymbol{y}))\) autour du mode \(\hat{\theta}\) donne : \[ \log(p(\theta|\boldsymbol{y})) = \log(p(\hat{\theta}|\boldsymbol{y})) + \frac{1}{2}(\theta-\hat{\theta})^T\left[\frac{\partial^2\log(p(\theta|\boldsymbol{y}))}{\partial \theta^2}\right]_{\theta=\hat{\theta}}(\theta-\hat{\theta}) + \dots\] On note que le terme linéaire (omis ci-dessus) est nul, puisque la dérivée de \(p(\theta|\boldsymbol{y})\) est nulle en son mode (\(\hat{\theta}\)). Le premier terme est lui constant en \(\theta\). Donc, en négligeant les termes suivants du développement, le logarithme de \(p(\theta|\boldsymbol{y})\) est égal au logarithme d’une densité gaussienne d’espérance \(\hat{\theta}\) et de variance \(I(\hat{\theta})^{-1}\) (où \(\textstyle I(\theta) = \left.\frac{\partial^2\log(p(\theta|\boldsymbol{y}))}{\partial \theta^2}\right|_{\theta=\hat{\theta}}\)), et l’on peut donc écrire l’approximation : \[p(\theta|\boldsymbol{y}) \approx \mathcal{N}(\hat{\theta}, I(\hat{\theta})^{-1})\]
Ce résultat a une double importance :
il peut être utilisé pour expliquer pourquoi les procédures bayésienne et fréquentiste basées sur le maximum de vraisemblance donnent, pour \(n\) grand, des résultats très voisins. Ainsi, en dimension 1, l’intervalle de crédibilité asymptotique est : \([\hat{\theta} \pm 1.96 \sqrt{I(\hat{\theta})^{-1}}]\), et si on le compare à l’intervalle de confiance fréquentiste construit à partir de la loi asymptotique de l’estimateur du maximum de vraisemblance : \([\hat{\theta}_{MLE} \pm 1.96 \sqrt{I(\hat{\theta}_{MLE})^{-1}}]\) (où \(I(\hat{\theta}_{MLE})\) est ici la matrice d’information de Fisher observée). On note que l’intervalle de confiance précédent est donc identique à l’intervalle de crédibilité asymptotique du MAP pour des lois a priori uniformes. Pour ces lois a priori, on note également que \(\hat{\theta} = \hat{\theta}_{MLE}\) (et même si on ne prend pas des a priori uniformes, les estimateurs et intervalles sont très proches, puisque le poids de la loi a priori devient négligeable quand \(n \rightarrow \infty\)). L’interprétation théorique de ces intervalles reste évidemment différente.
il signifie que l’on peut approximer la distribution a posteriori par une loi normale, dont on peut calculer l’espérance et la variance simplement à l’aide du MAP, et permet donc de faciliter les calculs numériques de l’inférence bayésienne.