Construction d'un modèle bayésien
La première étape dans la construction d’un modèle est toujours d’identifier la question à laquelle on souhaite répondre. Une fois cette étape accomplie, il s’agit de déterminer quelles observations sont disponibles, et vont pouvoir nous informer dans notre réponse à la question d’intérêt.
Modèle d’échantillonnage
Notons \(\boldsymbol{y}\) les observations dont nous disposons. De la même manière que dans un modèle fréquentiste, une modélisation bayésienne paramétrique consiste à d’abord proposer un modèle probabiliste pour ces observations : \(Y_i\overset{iid}{\sim} f(y|\theta)\). On appelle ce dernier “modèle d’échantillonnage.”
👉 Dans l’application historique, Laplace a proposé un modèle d’échantillonnage basé sur la loi …
…
…
Distribution a priori
Dans la modélisation bayésienne, par rapport à la modélisation fréquentiste, on ajoute une loi de probabilité (définie sur l’espace \(\Theta\) des paramètres), appelée distribution a priori : \[\begin{align*} \theta &\sim \pi(\theta)\\ Y_i|\theta &\overset{iid}{\sim} f(y|\theta) \end{align*}\] On va donc traiter \(\theta\) comme une variable aléatoire, mais qui n’est jamais observée !
👉 Dans l’application historique, Laplace a d’abord envisagé un a priori …
…
…
Distribution a posteriori
L’objet d’une telle modélisation bayésienne est la distribution des paramètres a posteriori, c’est-à-dire la loi de \(\theta\) conditionnellement aux observations : \(p(\theta|\boldsymbol{Y} = \boldsymbol{y})\), appelée distribution a posteriori. Elle se calcule à partir du modèle d’échantillonnage \(f(y|\theta)\) — à partir duquel on obtient la vraisemblance \(f(\boldsymbol{y}|\theta)\) pour toutes les observations — et de la loi a priori \(\pi(\theta)\) par le théorème de Bayes : \[p(\theta|\boldsymbol{y}) = \frac{f(\boldsymbol{y}|\theta)\pi(\theta)}{f(\boldsymbol{y})}\] où \(f(\boldsymbol{y}) = \int f(\boldsymbol{y}|\theta)\pi(\theta)\,\text{d}\theta\) est la loi marginale de \(\boldsymbol{Y}\).
Exemple avec un a priori uniforme
👉 Dans l’application historique, la vraisemblance est donc : …
…
…
…
👉 On obtient alors la loi a posteriori suivante : …
…
…
…
…
Malheureusement, cette intégrale (dite “incomplète”) n’a pas de solution analytique.
Une approximation par la loi normale a cependant permis à Laplace de conclure que la probabilité de naissance d’un fille est inférieure à celle d’un garçon,1 puisqu’il obtint : \(P(\theta\geq 0.5|\boldsymbol{y})\approx 1.15~10^{-42}\)
Exemple de la conjugaison de la loi Beta
Imaginons maintenant que l’on utilise une autre loi a priori, par exemple la loi \(\text{Beta}(\alpha, \beta)\) dont la densité s’écrit : \(\forall\,0\leq\theta\leq1 \, ,\) \(\textstyle f(\theta)=\frac{(\alpha +\beta -1)!}{(\alpha-1)!(\beta -1)!}\theta^{\alpha-1}(1-\theta)^{\beta-1}\) (pour \(\alpha >0\) et \(\beta>0\)).
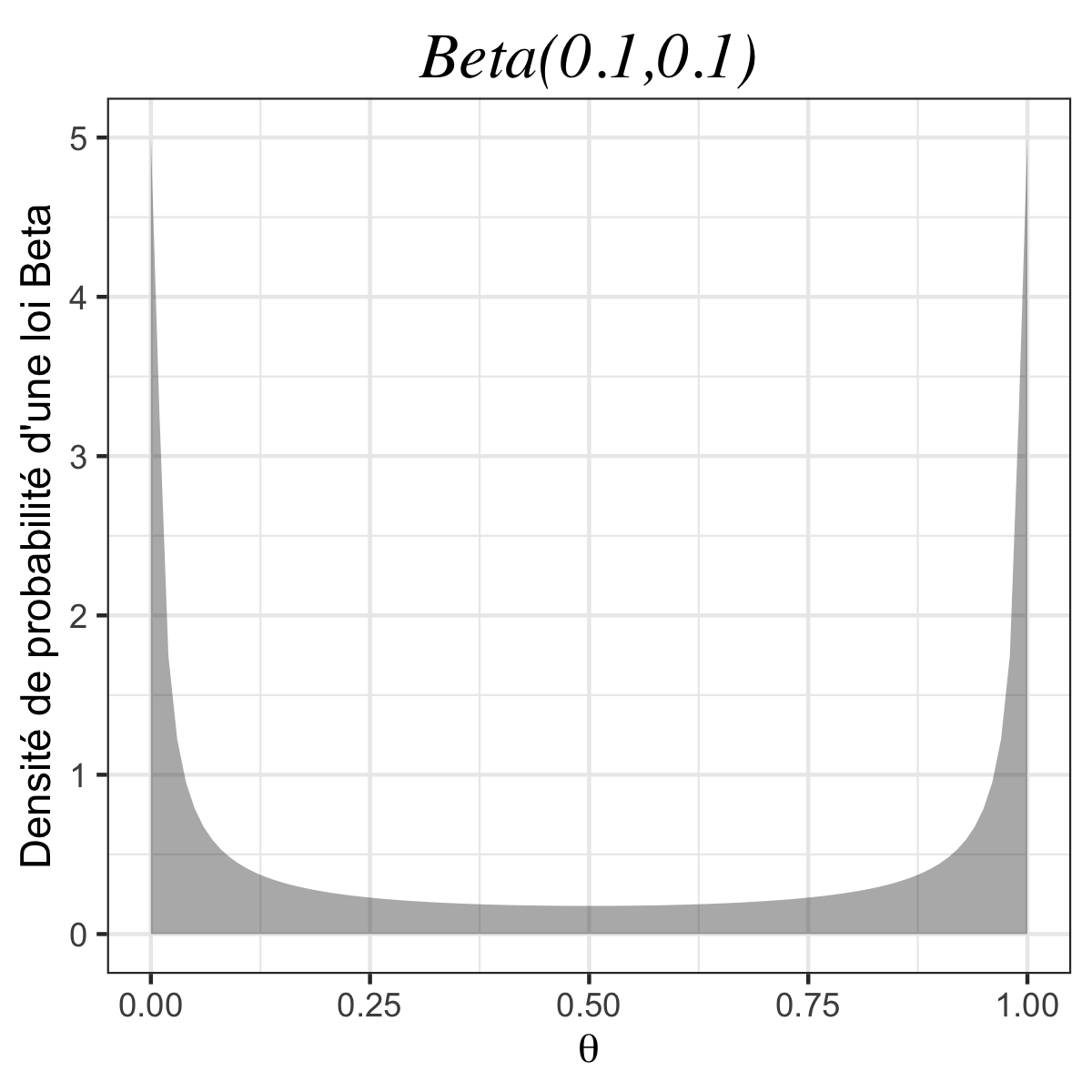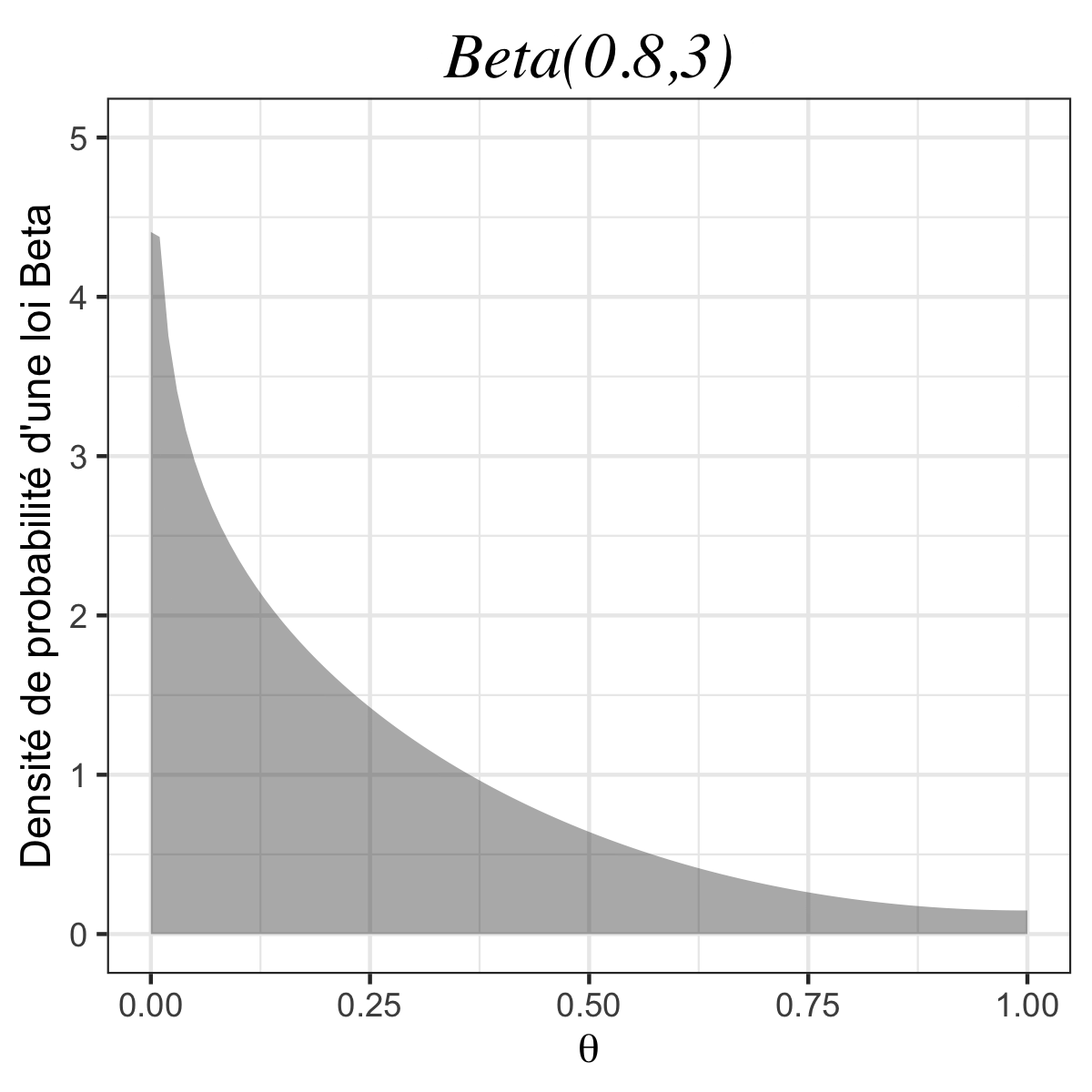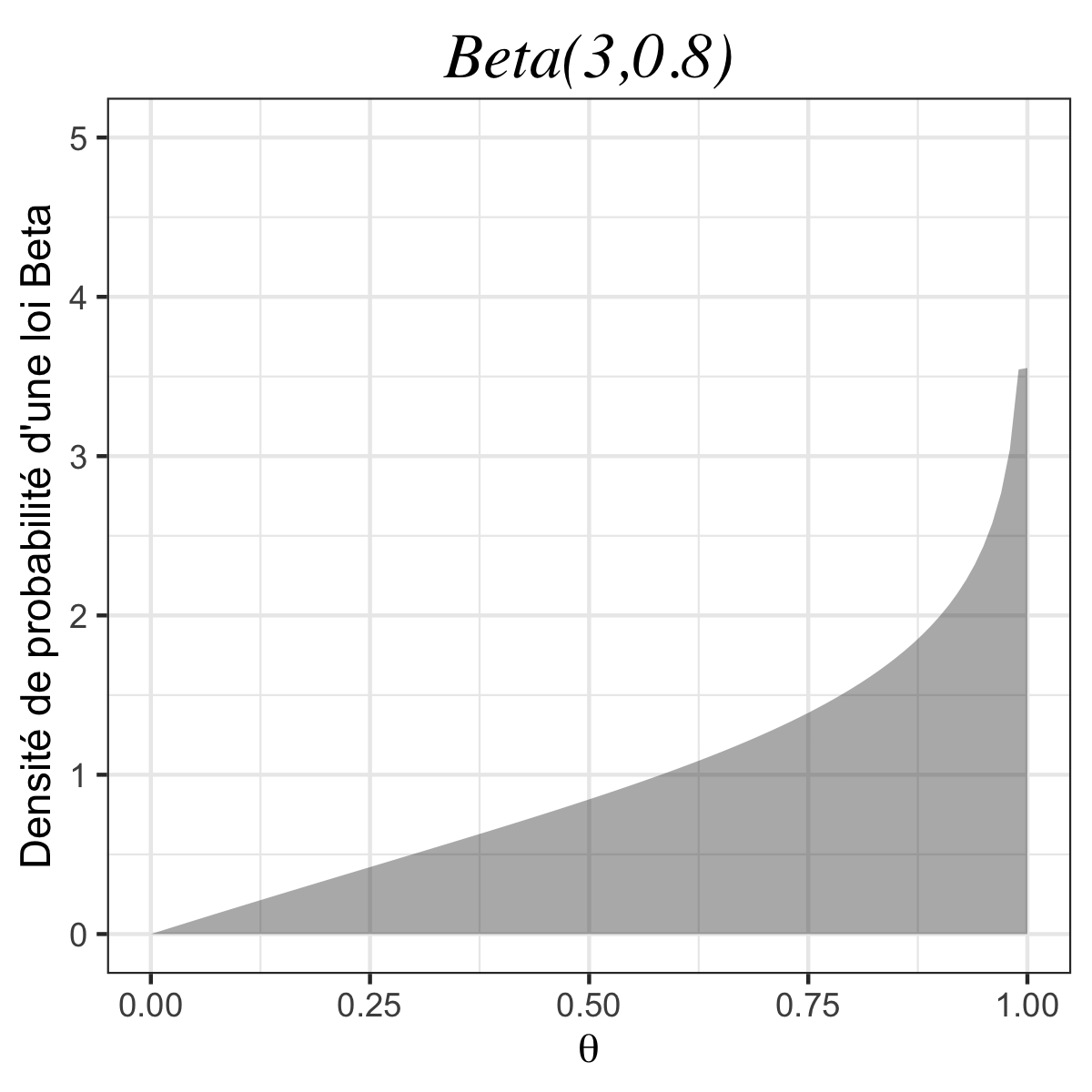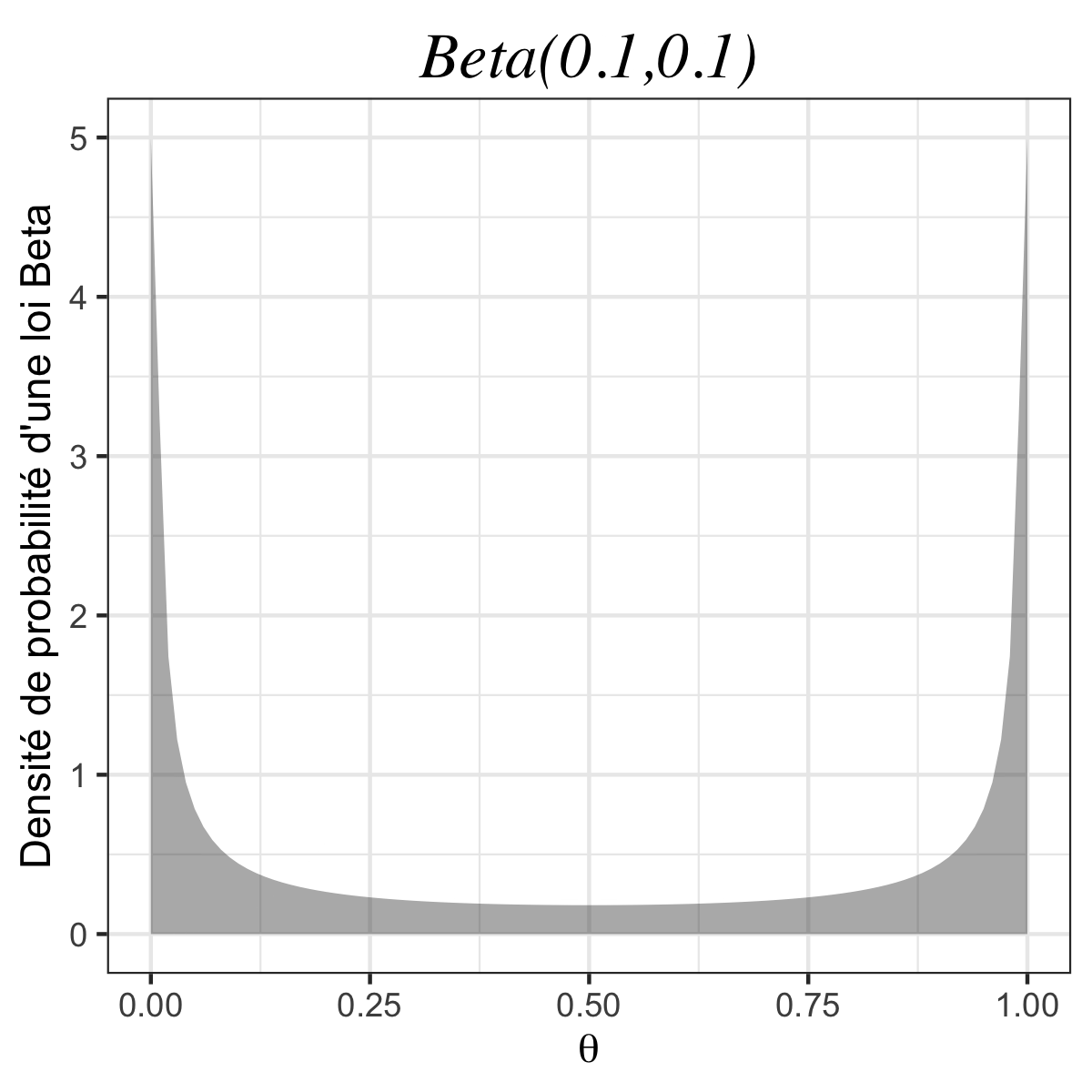
👉 On remarque que la loi uniforme est un cas particulier de la loi Beta lorsque \(\alpha\) et \(\beta\) valent tous les deux 1. Si on re-calcule le posterior avec un a priori \(\pi = \text{Beta}(\alpha, \beta)\), on obtient facilement :
…
👉 On reconnait, à une constante de normalisation près la densité …
…
👉 On en déduit donc que …
\(\theta|\textbf{y}\sim\) …
On dit que l’on est dans une situation de distributions conjuguées car les distributions a posteriori et a priori appartiennent à la même famille paramétrique.
On peut maintenant évaluer l’impact de cet a priori Beta sur notre résultat en fonction du choix des hyperparamètres \(\alpha\) et \(\beta\).
| Interprétation de l’a priori | Paramètres de la Beta | \(P(\theta\geq 0,5|\boldsymbol{y})\) |
|---|---|---|
| #garçons \(>\) #filles | \(\alpha=0,1; \beta=3\) | \(1,08~10^{-42}\) |
| #garçons \(<\) #filles | \(\alpha=3\phantom{,1};\beta=0.1\) | \(1,19~10^{-42}\) |
| #garçons \(=\) #filles | \(\alpha=4\phantom{,1};\beta=4\) | \(1,15~10^{-42}\) |
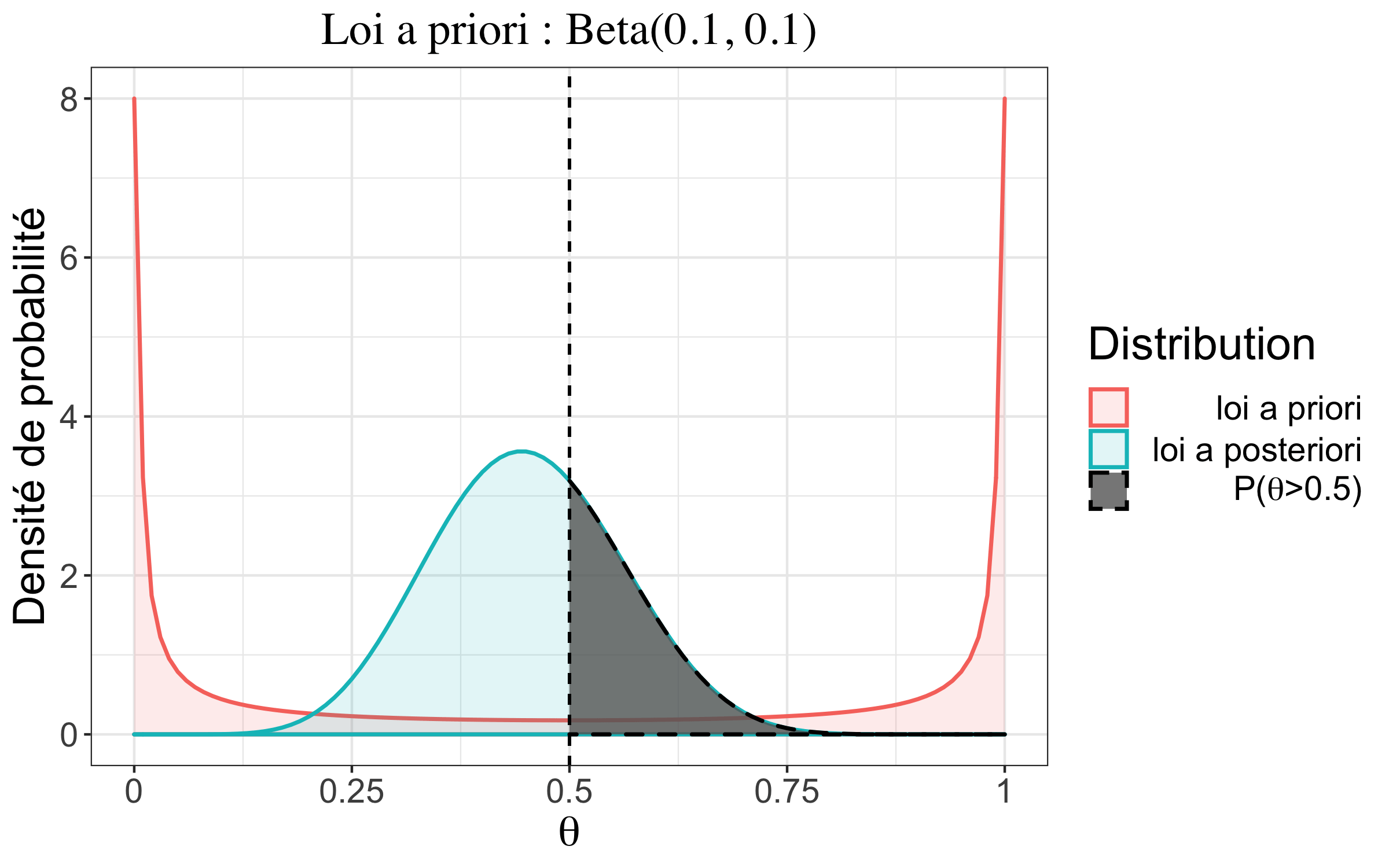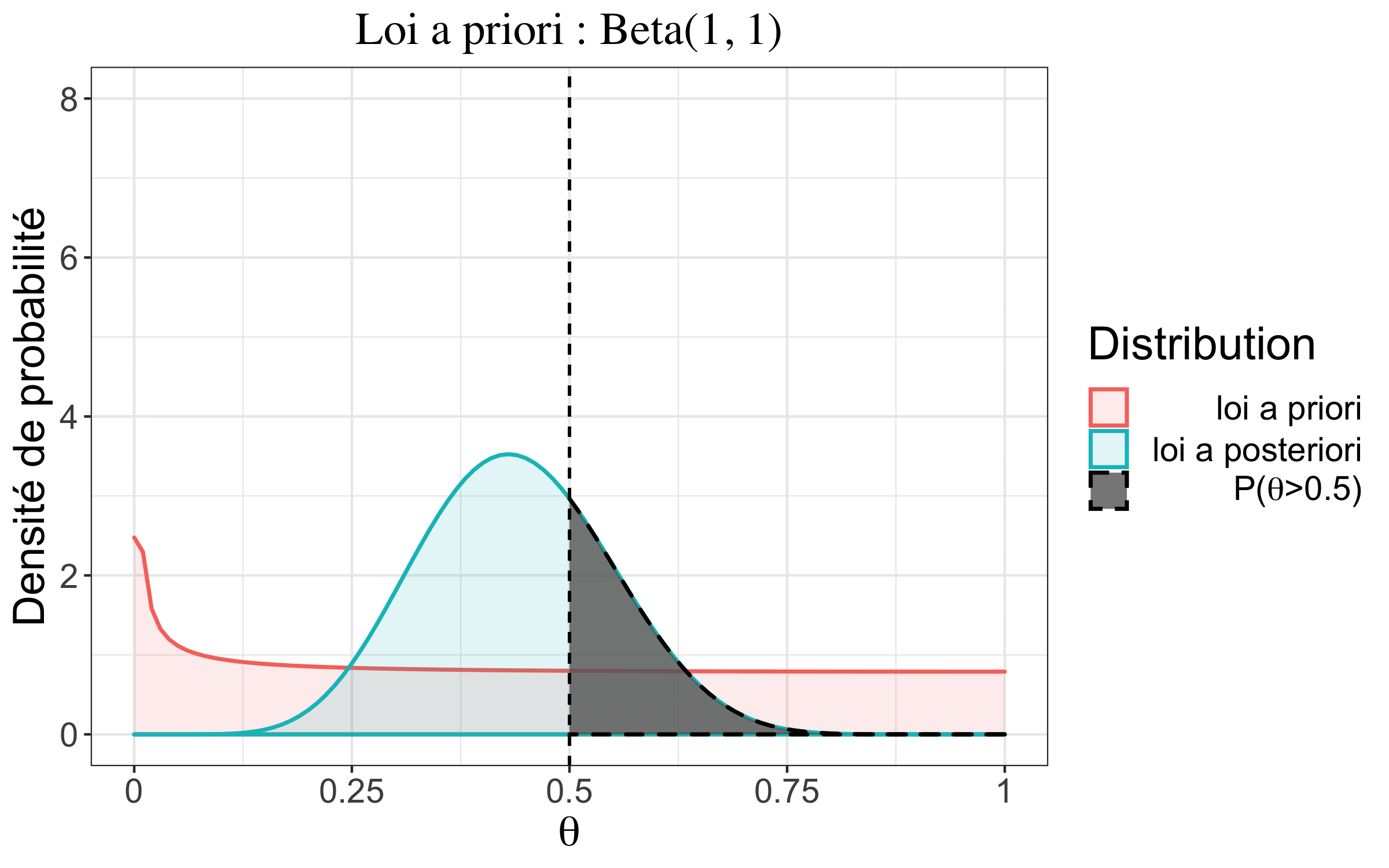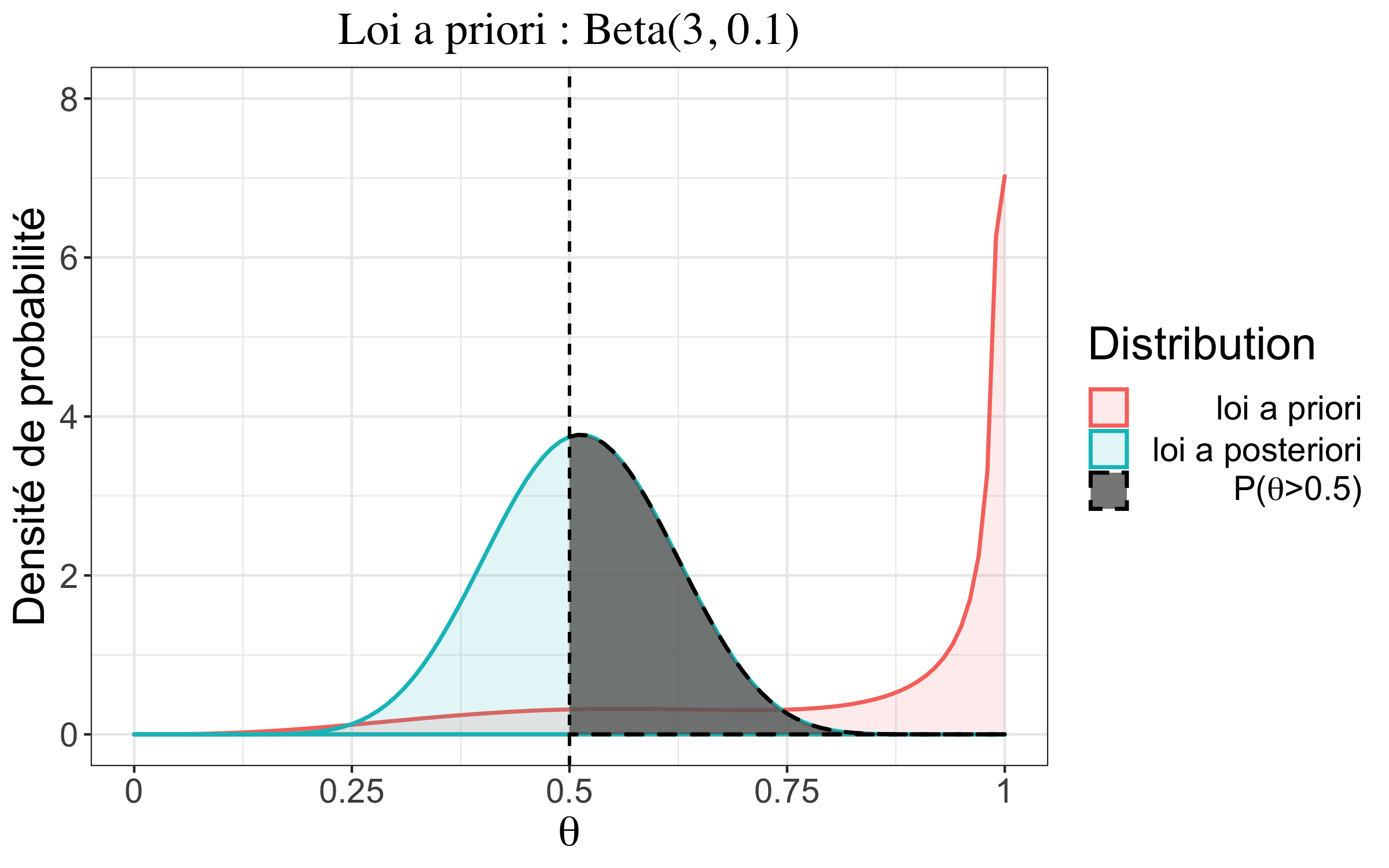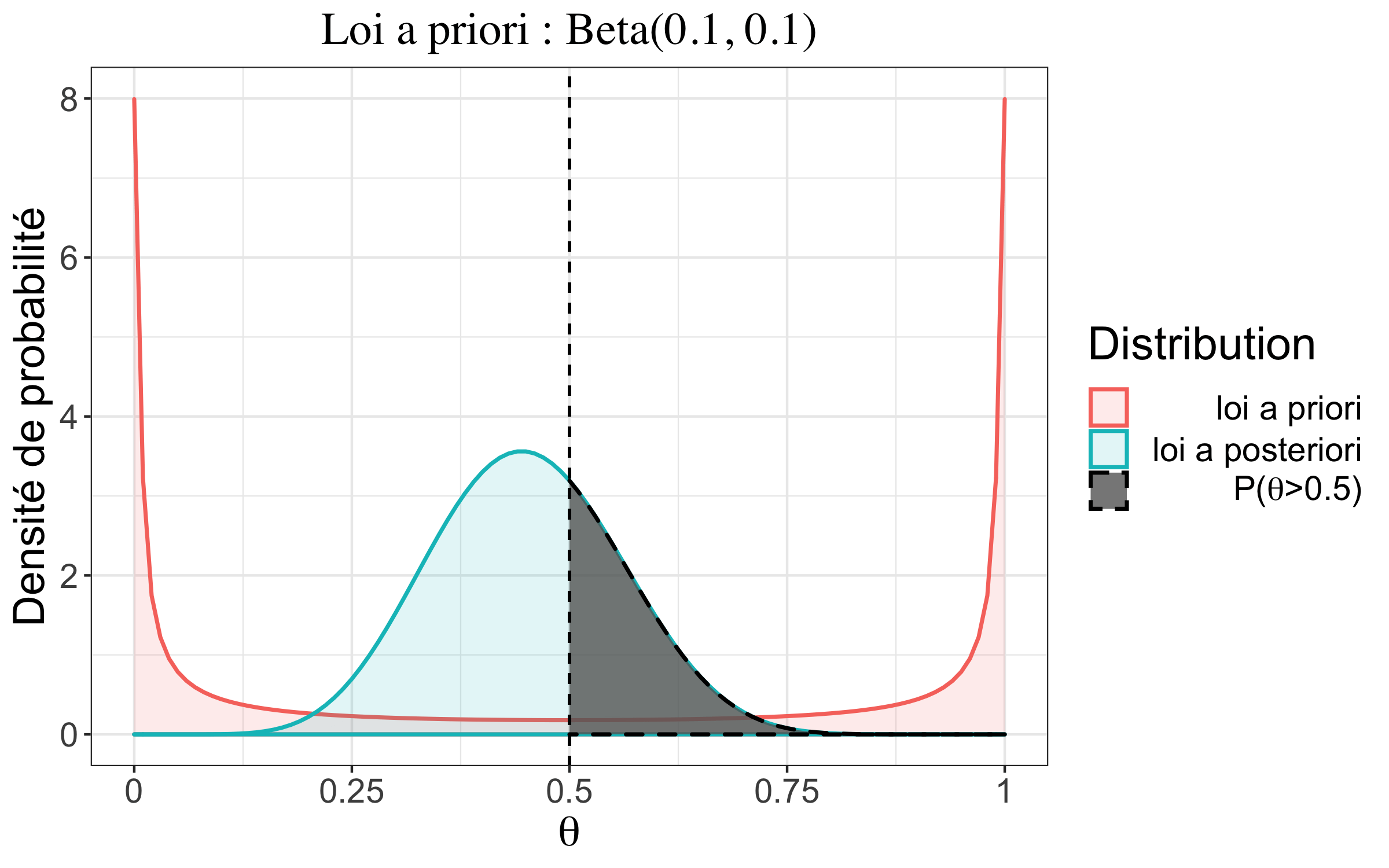
| #garçons \(\neq\) #filles | \(\alpha=0,1;\beta=0.1\) | \(1,15~10^{-42}\) |
| non informatif | \(\alpha=1\phantom{,1};\beta=1\) | \(1,15~10^{-42}\) |
On remarque que l’a priori ne semble pas influer sur notre résultat ici. C’est parce que l’on dispose de beaucoup d’observations. Le poids de la distribution a priori dans la ditribution a posteriori devient alors très faible en regard de l’information apportée par les observations. Si l’on imagine que l’on avait observé seulement 20 naissances, dont 9 filles, on note alors une influence de l’a priori bien plus grande.
| Interprétation de l’a priori | Paramètres de la Beta | \(P(\theta\geq 0,5|\boldsymbol{y})\) |
|---|---|---|
| #garçons \(>\) #filles | \(\alpha=0,1; \beta=3\) | \(0,39\) |
| #garçons \(<\) #filles | \(\alpha=3\phantom{,1};\beta=0,1\) | \(0,52\) |
| #garçons \(=\) #filles | \(\alpha=4\phantom{,1};\beta=4\) | \(0,46\) |
| #garçons \(\neq\) #filles | \(\alpha=0,1;\beta=0,1\) | \(0,45\) |
| non informatif | \(\alpha=1\phantom{,1};\beta=1\) | \(0,45\) |
La question épineuse du choix de la distribution a priori
Un point essentiel de l’approche bayésienne est donc de donner une distribution aux paramètres. Dans l’inférence bayésienne, on part d’une distribution a priori, et l’information contenue dans les observations est utilisée pour obtenir la distribution a posteriori. La distribution a priori apporte de la flexibilité par rapport à un modèle fréquentiste, en permettant d’incorporer dans le modèle de la connaissance externe. Cela peut par exemple permettre de résoudre des problèmes d’identifiabilité parfois rencontrés par une approche purement fréquentiste lorsque l’information apportée par les observations ne suffit pas pour estimer tous les paramètres d’intérêt.
C’est donc un grand avantage de l’approche bayésienne. Mais d’un autre côté, le choix de cette distribution a priori des paramètres introduit une subjectivité intrinsèque dans l’analyse, qui peut être décriée. Par exemple un statisticien travaillant pour un laboratoire pharmaceutique pourrait choisir une loi a priori donnant une forte probabilité qu’un médicament soit efficace, ce qui influencera nécessairement le résultat. Le choix (ou l’élicitation) de la distribution a priori est donc délicat.
Notons tout d’abord deux points théoriques :
- le support de la distribution a posteriori doit être inclus dans celui de la distribution a priori. En d’autres termes, si \(\pi(\theta) = 0\), alors \(p(\theta|\boldsymbol{y}) = 0\).
- en général on suppose l’indépendance des différents paramètres sous la loi a priori (quand il y a plus d’un paramètre — ce qui est presque toujours le cas dans les applications) ce qui permet d’éliciter les lois a priori paramètre par paramètre.
Élicitation de la distribution a priori
Il y a des stratégies pour communiquer avec les experts non-statisticiens pour transformer leurs connaissances a priori en distribution a priori.
La méthode la plus simple est de demander aux experts de donner des poids ou des probabilités à des intervalles de valeurs : c’est la méthode des histogrammes. Cependant, quand le paramètre peut prendre des valeurs sur un ensemble non-borné cette méthode risque de donner un a priori nul pour des valeurs du paramètre qui sont néanmoins possibles…
Une autre approche est de se donner une famille paramétrique de distributions \(p(\theta|\eta)\) et de choisir \(\eta\) de telle sorte que la distribution a priori soit en accord avec ce que pensent les experts pour certaines caractéristiques. Par exemple on pourra faire en sorte que les deux premiers moments (moyenne et variance), ou bien des quantiles simples (comme les quartiles), coïncident avec leurs vues. Cela résout le problème de support soulevé par la méthode des histogrammes. Cependant le choix de la famille paramétrique peut avoir de l’importance. Par exemple une distribution normale \(\mathcal{N}(0 ; \text{2,19})\) a les mêmes quartiles qu’une distribution de Cauchy \(\mathcal{C}(0;1)\), à savoir \(-1;0;1\). Or ces deux lois a priori peuvent donner des distributions a posteriori assez différentes. Une stratégie pour déterminer les quartiles est de poser les questions suivantes :
- pour la médiane : Pouvez-vous déterminer une valeur telle que \(\theta\) a autant de chances de se trouver au-dessus qu’en-dessous ?
- puis pour le premier quartile : Supposons que l’on vous dise que \(\theta\) est en dessous de [telle valeur médiane], pouvez-vous alors déterminer une nouvelle valeur telle que \(\theta\) ait autant de chances de se trouver au-dessus qu’en-dessous ?
- de façon similaire on détermine le troisième quartile…
Des logiciels existent pour aider à l’élicitation des lois a priori par des experts : voir par exemple l’outil académique SHELF2 3.
On peut également éliciter des lois a priori d’après les données de la littérature. L’idée est de définir les moments de la distribution a priori tels qu’ils donnent une probabilité raisonnable aux valeurs du paramètre qui ont été recensées dans la littérature. Si on propose un a priori normal de loi \(\mathcal{N}(\mu, \sigma^2)\), on peut par exemple choisir \(\mu\) et \(\sigma\) de telle sorte que la plus petite valeur donnée dans la littérature soit égale à \(\mu - 1.96\sigma\) et la plus grande à \(\mu + 1.96\sigma\) . Une approche plus élaborée est de maximiser la vraisemblance des valeurs de la littérature…
La quête des a priori non-informatifs
Pour certains paramètres (ou pour tous les paramètres) il est courant que l’on n’ait pas de connaissance a priori. On cherche alors à définir une distribution “non-informative.” Par exemple si le paramètre est la probabilité qu’un pièce de monnaie tombe sur pile ou face, une loi non-informative pourrait être la loi uniforme sur [0;1] (le choix historique de Bayes en 1763). Cependant deux difficultés majeures apparaissent :
- Lois impropres
La première difficulté est que l’on peut être amené à considérer des lois impropres. Une loi impropre est définie par une densité de probabilité dont l’intégrale ne somme pas à 1. Par exemple pour un paramètre de moyenne d’une loi normale, il peut semble naturel de donner une densité constante \(\pi(\theta) = c\) (i.e. toutes les valeurs possibles sur \(]-\infty, +\infty[\) ont la même probabilité). Bien sûr \(\int_{-\infty}^\infty c\,\text{d}\theta = \infty\), et un tel choix ne définit donc pas une loi de probabilité ! Il reste cependant admissible car la loi a posteriori est (la plupart du temps) propre. En effet nous avons alors : \[p(\theta|y) = \frac{f(y|\theta)\cancel{c}}{\int f(y|\theta)\cancel{c}\,\text{d}\theta}\] Si \(\int f(y|\theta)\,\text{d}\theta = K\) (comme c’est souvent le cas), alors \(\textstyle p(\theta|y) = \frac{f(y|\theta)}{K}\) est une densité propre (i.e. qui somme à \(1\)).
- Lois non-invariantes
La seconde difficulté vient de la non-invariance de la distribution uniforme pour des transformations non-linéaires des paramètres. En effet si on fait une transformation des paramètres \(\gamma = g(\theta)\) la densité de \(\gamma\) s’écrit : \(\pi(\gamma) = |J|\,\pi(\theta)\), où \(|J|\) est le Jacobien de la transformation, c’est-à-dire le déterminant de la matrice jacobienne \(\textstyle J = \frac{\partial g^{-1}(\gamma)}{\partial \gamma}\). Par exemple si on prend un a priori uniforme égale à 1 pour \(\theta\) sur \((0, +\infty)\) et que l’on fait la transformation \(\gamma = \log(\theta)\), on a \(g^{-1}(\gamma) = e^\gamma\) et \(|J| = e^\gamma\). Donc on a \(\pi(\gamma) = e^\gamma\), ce qui n’est pas la caractérisation d’une loi uniforme. D’où le paradoxe suivant : si la loi uniforme pour \(\theta\) traduit une absence totale de connaissance a priori sur \(\theta\), on devrait avoir aussi une absence totale d’information a priori sur \(\gamma\), ce qui devrait se traduire par une loi uniforme sur \(\gamma\). Or ce ne peut être le cas. Donc la loi uniforme ne peut pas être d’une manière générale la loi représentant une absence totale de connaissance a priori. C’est un argument central qui a conduit Fisher, en 1922, à proposer les estimateurs du maximum de vraisemblance, possédant eux une propriété d’invariance pour des transformations non-linéaires des paramètres.
Démonstration : Soit \(F_X(x) = P(X < x)\) et considérons la transformation non linéaire \(Y = g(X)\). On a alors \(F_Y(y) = P(Y < y) = P(g(X) < y) = P(X < g^{-1}(y))\). La densité s’obtient naturellement en dérivant par rapport à \(y\) : \(\textstyle f_Y (y) = \frac{\partial g^{-1}(y)}{\partial y}f_X (g^{-1}(y))\). La formule s’étend au cas multidimensionnel où \(|J|\) désigne le déterminant de la matrice jacobienne \(J\) (matrice des dérivées partielles).
NB : Ceci ne veut pas dire que l’on ne puisse pas prendre une loi uniforme comme a priori, mais il faut avoir conscience que la loi uniforme ne vaut que pour une certaine paramétrisation…
Face à ces difficultés, différentes solutions ont été proposées. Elles ont montré qu’il n’y a pas de loi a priori complètement non-informative, mais on peut considérer certaines lois comme faiblement informatives.
La loi a priori de Jeffreys
L’approche la plus aboutie des a priori faiblement informatifs est peut-être celle de Jeffreys. Ce dernier a proposé une procédure pour trouver une loi a priori avec une propriété d’invariance par rapport à la paramétrisation. Dans le cas univarié, la loi a priori de Jeffreys est défini par : \[\pi(\theta) \propto \sqrt{I(\theta)}\] où \(I\) est la matrice d’information de Fisher (pour rappel, \(\textstyle I(\theta) = -\mathbb{E}_{Y|\theta}\left[\frac{\partial^2 \log (f(y|\theta))}{\partial\theta^2}\right]\)). La loi a priori de Jeffreys est invariante pour les transformations bijectives des paramètres. C’est-à-dire que si nous considérons une autre paramétrisation \(\gamma = g(\theta)\) (pour laquelle il existe la bijection réciproque \(g^{-1}(\cdot)\)), on obtient toujours : \[\pi'(\gamma) \propto \sqrt{I(\gamma)}\] tandis que \(\pi'(\gamma)\) induit bien la même loi a priori sur \(\theta\) que \(\pi(\theta)\). Prenons ici des notations plus rigoureuses, et notons les densités \(\pi_\theta(\cdot)\) et \(\pi_\gamma(\cdot)\). \(\pi_\gamma(\cdot)\) s’exprime en fonction de \(\pi_\theta(\cdot)\) avec \(\pi_\gamma(\cdot) = \pi_\theta(\cdot)|J|\). On vérifie donc bien que \(\textstyle\sqrt{I(\gamma)} = \sqrt{I(\theta)}|J|\).
Dans le cas multidimensionnel (le plus courant) la loi a priori de Jeffreys est définie comme : \[\pi(\theta) \propto \sqrt{ | I(\theta) | }\] où \(|I(\theta)|\) est le déterminant de la matrice d’information de Fisher \(I(\theta)\). Cependant cette méthode est peu utilisée car d’une part les calculs peuvent être compliqués, et d’autre part elle peut donner des résultats un peu curieux. En effet dans le cas d’une vraisemblance normale par exemple, où l’on a 2 paramètres \(\theta\) et \(\sigma\), l’a priori de Jeffreys multidimensionnel est \(1/\sigma^2\), ce qui est différent de \(\pi(\sigma) \propto 1/\sigma\) obtenu dans le cas unidimensionnel… Dans la pratique la tendance est d’appliquer la loi a priori de Jeffreys séparément pour chaque paramètre et de définir la loi a priori conjointe par la multiplication des a priori pour chaque paramètre (faisant donc une hypothèse d’indépendance). Pour l’exemple normal avec deux paramètres, on obtient donc \(\pi(\theta,\sigma) \propto 1/\sigma\). Mais on note que ce n’est plus vraiment l’a priori de Jeffreys, en deux dimensions.
Exercice : retrouver les résultats énoncés ci-dessus (invariance pour la transformation \(\log\) et résultat pour la loi normale).
- Loi a priori pour les familles à paramètres de position et d’échelle :
Considérons les familles à paramètre de position, c’est-à-dire dont les modèles d’échantillonnage sont de la forme \(f(y|\theta) = f(y - \theta)\). Des arguments d’invariance permettent d’affirmer que la loi non-informative pour \(\theta\) devrait être uniforme. Par les mêmes arguments, on montre que pour les familles à paramètre d’échelle, c’est-à-dire dont les modèles d’échantillonnage sont de la forme \(f(y|\sigma) = f(y/\sigma)\), la loi non-informative devrait être \(\pi(\sigma) \propto 1/\sigma\). Plus généralement, pour les familles à paramètres de position et d’échelle, c’est-à-dire dont les modèles d’échantillonnage sont de la forme \(f(y|\theta,\sigma) = f((y - \theta)/\sigma)\), l’a priori faiblement-informatif devrait être de la forme \(\pi(\theta, \sigma) = 1/\sigma\). La loi normale est une famille de ce type, et pour elle cette recommandation d’a priori faiblement-informatif rejoint celle obtenue en multipliant les a priori de Jeffreys unidimensionnels, ainsi qu’indiqué plus haut.
Exercice : retrouver les résultats énoncés ci-dessus.
Lois a priori diffuses
En pratique, une alternative très courante pour donner une loi a priori faiblement informative est l’utilisation de lois paramétriques (telles que la loi normale) avec des paramètres de variances très importants (ce qui se rapproche de la loi uniforme mais évite le problème de loi impropre).
Cette conclusion a été confirmée depuis et semble être valable pour l’espèce humaine en général.↩︎